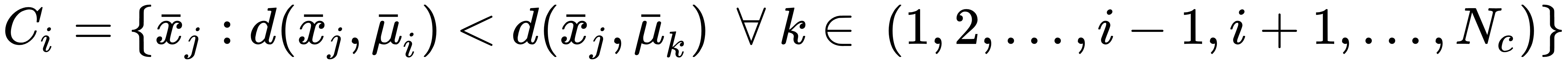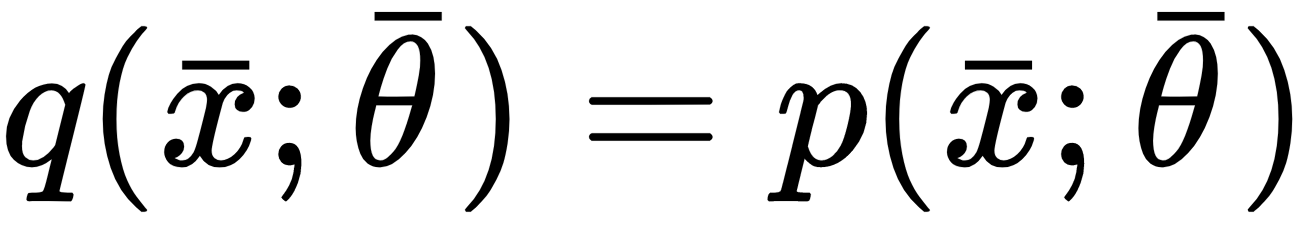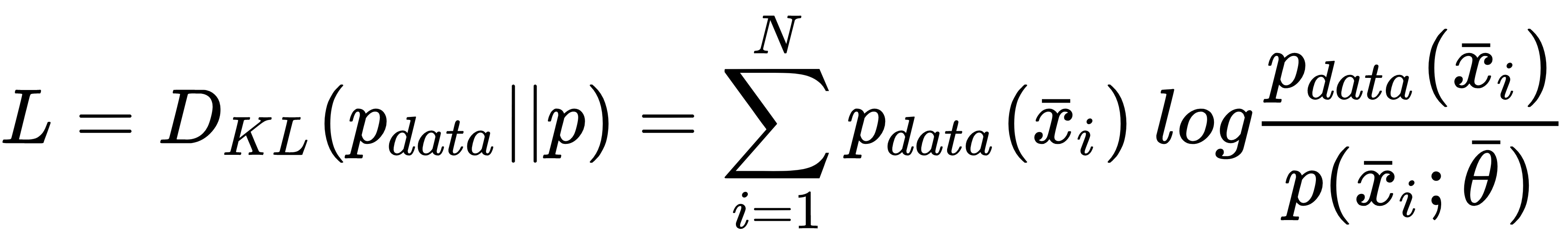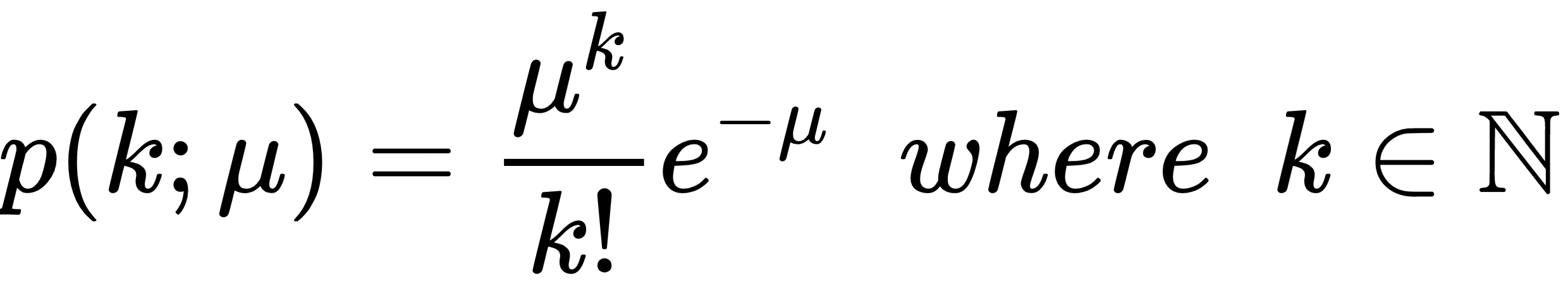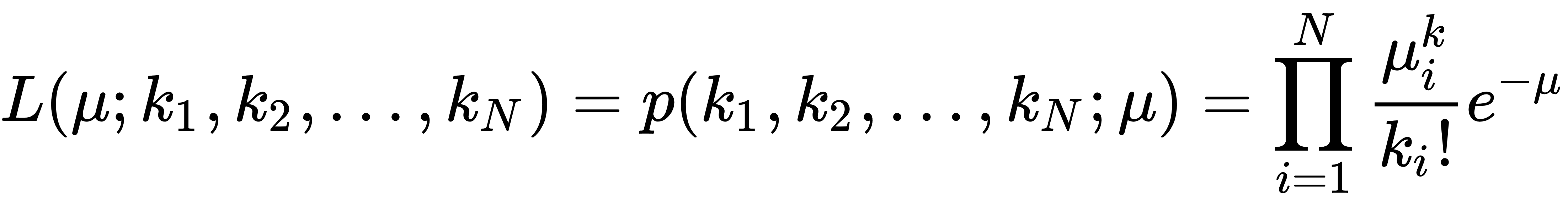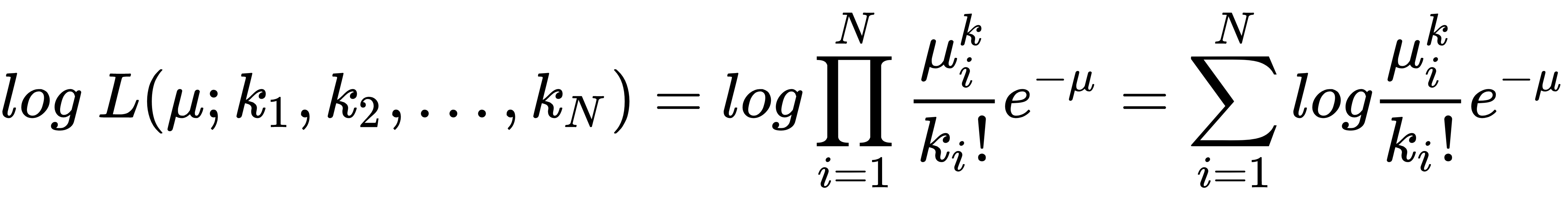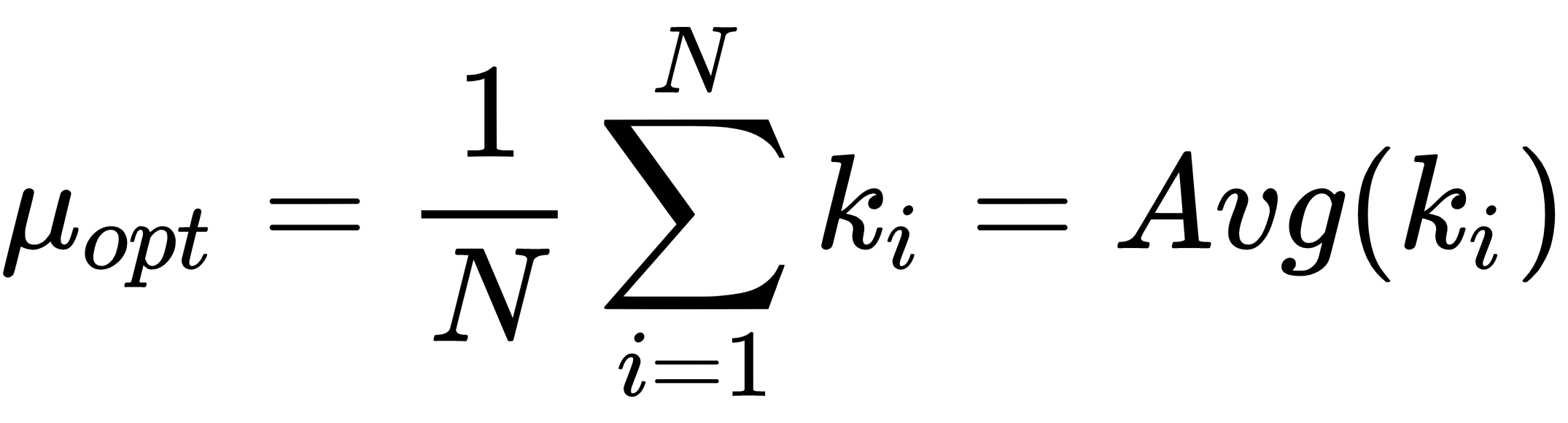As this book is completely dedicated to unsupervised algorithms, I've decided not to show a simple cluster analysis as a hello world! example, but rather a quite basic generative model. Let's assume that we are monitoring the number of trains that arrive at a subway station every hour because we need to ascertain the number of security agents required at the station. In particular, we're asked to have at least one agent per train and whenever there are fewer, we're going to pay a fine.
Moreover, it's easier to send a group at the beginning of every hour instead of controlling the agents one by one. As the problem is very simple, we also know that a good distribution is the Poisson one, parameterized with μ, which is also the mean. From the theory, we know that such a distribution can effectively model the random number of events happening in a fixed time frame, under the main assumption of independence. In general cases, a generative model is based on a parameterized distribution (for example, with a neural network) and no specific assumptions are made about its family. Only in some particular cases (for example, Gaussian mixture), is it reasonable to pick distributions with particular properties and, without loss of rigor, we can consider this example as one such scenario.
The probability mass function of a Poisson distribution is:
This distribution describes the probability of observing k events in a predefined interval. In our case, the interval is always one hour and we're keen to estimate the probability of observing more than 10 trains. How can we obtain the correct figure for μ?
The most common strategy is called Maximum Likelihood Estimation (MLE). It collects a set of observations and finds the value of μ that maximizes the probability that all the points have been generated by our distribution.
Assuming we have collected N observations (each observation is the number of arrivals in one hour), the likelihood of μ with respect to all samples is the joint probability of all samples (for simplicity, assumed to be IID) under the probability distribution computed using μ:
As we are working with a product and exponential, it's a common rule to compute the log-likelihood:
Once the log-likelihood has been computed, it's possible to set the derivative with respect to μ equal to 0 in order to find the optimal value. In this case, we omit the proof (which is straightforward to obtain) and arrive directly at the MLE estimation of μ:
We are lucky! The MLE estimation is just the average of the arrival times. This means that, if we have observed N values with average μ, the Poisson distribution, which is the most likely to have generated them, has μ as the characteristic coefficient. Therefore, any other sample drawn from such a distribution will be compatible with the observed dataset.
We can now start with our first simulation. Let's assume we've collected 25 observations during the early afternoon of a business day, as follows:
import numpy as np
obs = np.array([7, 11, 9, 9, 8, 11, 9, 9, 8, 7, 11, 8, 9, 9, 11, 7, 10, 9, 10, 9, 7, 8, 9, 10, 13])
mu = np.mean(obs)
print('mu = {}'.format(mu))
The output of the last command is as follows:
mu = 9.12
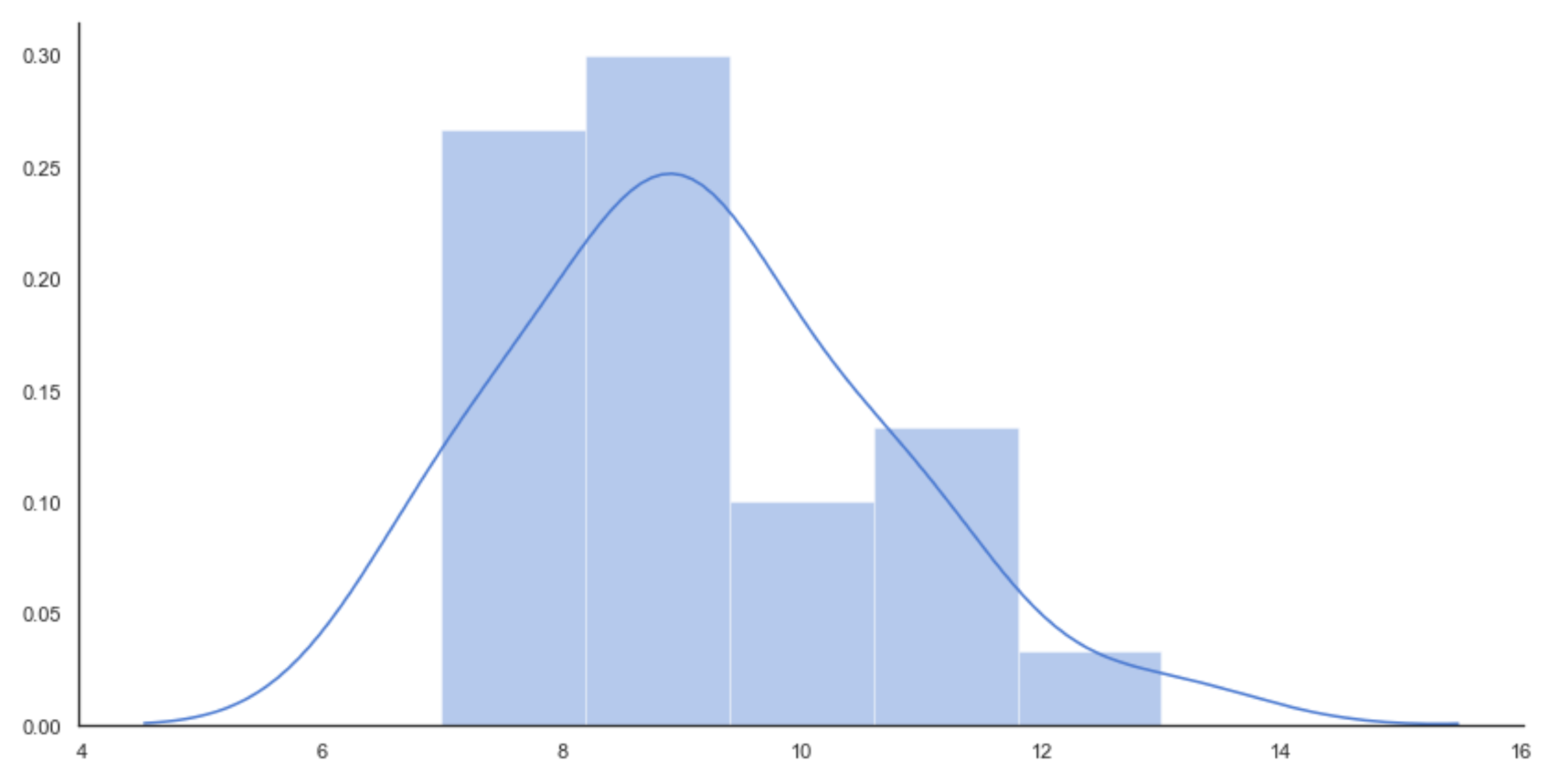
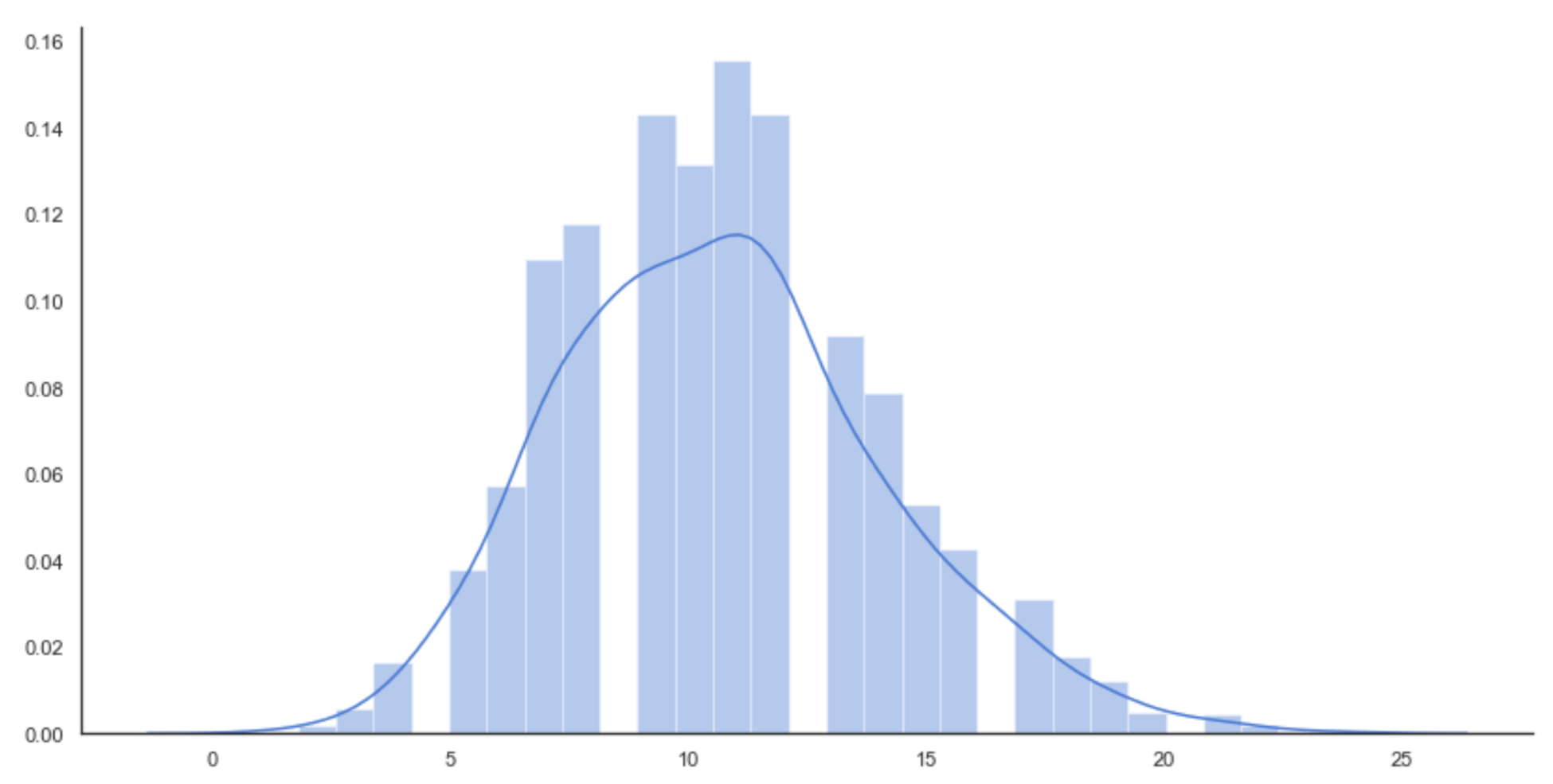
Hence, we have an arrival average of about nine trains per hour. The histogram is shown in the following diagram:
Histogram of the initial distribution
To compute the requested probabilities, we need to work with the Cumulative Distribution Function (CDF), which is implemented in SciPy (in the scipy.stats package). In particular, as we are interested in the probability of observing more trains than a fixed value, it's necessary to use the Survival Function (SF), which corresponds to 1-CDF, as follows:
from scipy.stats import poisson
print('P(more than 8 trains) = {}'.format(poisson.sf(8, mu)))
print('P(more than 9 trains) = {}'.format(poisson.sf(9, mu)))
print('P(more than 10 trains) = {}'.format(poisson.sf(10, mu)))
print('P(more than 11 trains) = {}'.format(poisson.sf(11, mu)))
The output of the preceding snippet is as follows:
P(more than 8 trains) = 0.5600494497386543
P(more than 9 trains) = 0.42839824517059516
P(more than 10 trains) = 0.30833234660452563
P(more than 11 trains) = 0.20878680161156604
As expected, the probability of observing more than 10 trains is low (30%) and it doesn't seem reasonable to send 10 agents. However, as our model is adaptive, we can continue collecting observations (for example, during the early morning), as follows:
new_obs = np.array([13, 14, 11, 10, 11, 13, 13, 9, 11, 14, 12, 11, 12, 14, 8, 13, 10, 14, 12, 13, 10, 9, 14, 13, 11, 14, 13, 14])
obs = np.concatenate([obs, new_obs])
mu = np.mean(obs)
print('mu = {}'.format(mu))
The new value for μ is as follows:
mu = 10.641509433962264
Now the average is almost 11 trains per hour. Assuming that we have collected enough samples (considering all potential accidents), we can re-estimate the probabilities, as follows:
print('P(more than 8 trains) = {}'.format(poisson.sf(8, mu)))
print('P(more than 9 trains) = {}'.format(poisson.sf(9, mu)))
print('P(more than 10 trains) = {}'.format(poisson.sf(10, mu)))
print('P(more than 11 trains) = {}'.format(poisson.sf(11, mu)))
The output is as follows:
P(more than 8 trains) = 0.7346243910180037
P(more than 9 trains) = 0.6193541369812121
P(more than 10 trains) = 0.49668918740243756
P(more than 11 trains) = 0.3780218948425254
With the new dataset, the probability of observing more than nine trains is about 62%, (which confirms our initial choice), but the probability of observing more than 10 trains is now about 50%. As we don't want to risk paying the fine (which is higher than the cost of an agent), it's always better to send a group of 10 agents. In order to get further confirmation, we have decided to sample 2,000 values from the distribution, as follows:
syn = poisson.rvs(mu, size=2000)
The corresponding histogram is shown in the following diagram:
Histogram of 2000 points sampled from the final Poisson distribution
The diagram confirms a peak slightly after 10 (very close to 11) and a rapid decay starting from k = 13, which has already been discovered using a limited dataset (compare the shapes of the histograms for further confirmation). However, in this case, we are generating potential samples that couldn't be present in our observation set. The MLE guarantees that the probability distribution is consistent with the data and that the new samples are weighted accordingly. This example is clearly extremely simple and its goal was only to show the dynamics of a generative model.
We are going to discuss many other more complex models and examples in the next chapters of the book. One important technique, common to many algorithms lies in not picking a predefined distribution (which implies an apriori knowledge) but rather in using flexible parametric models (for example, neural networks) to find out the optimal distribution. The choice of a predefined prior (as in this case) is justified only when there's a high confidence degree about the underlying stochastic process. In all other situations, it's always preferable to avoid any assumption and rely only on the data in order to find the most appropriate approximation of the data generating process.



 Free Chapter
Free Chapter

 the dataset is obtained as:
the dataset is obtained as:
 can be modeled in two ways:
can be modeled in two ways: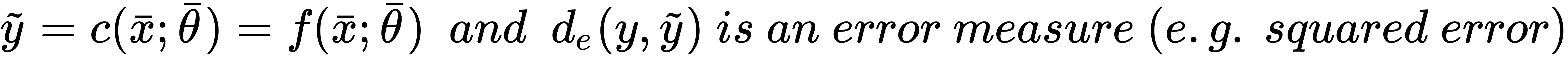
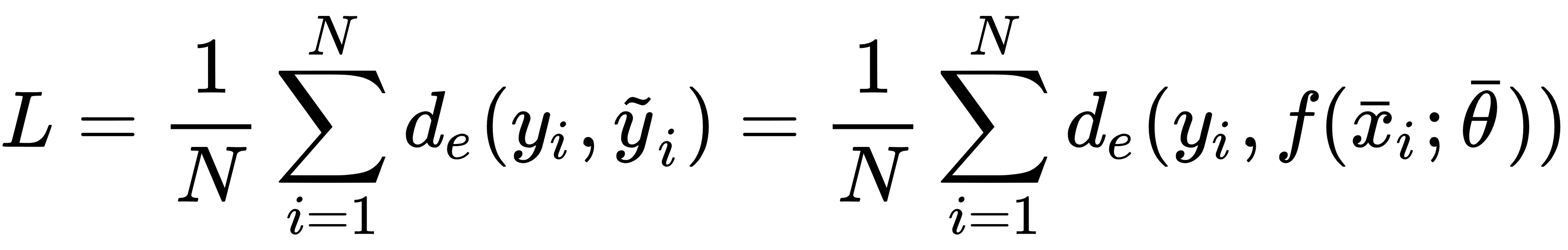
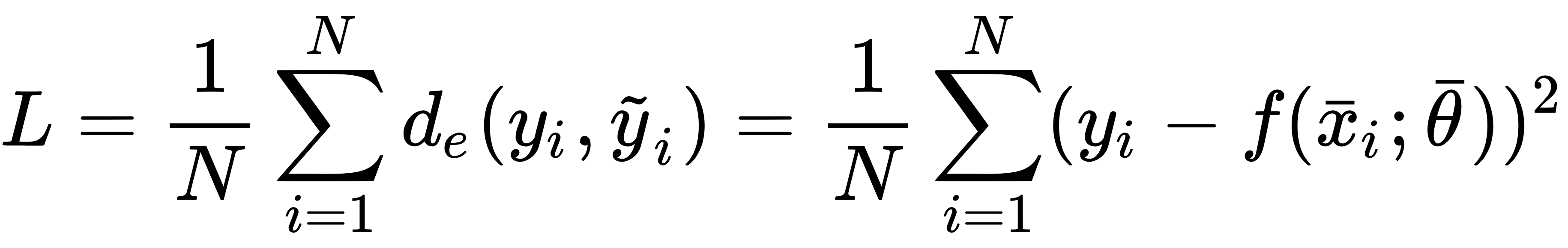
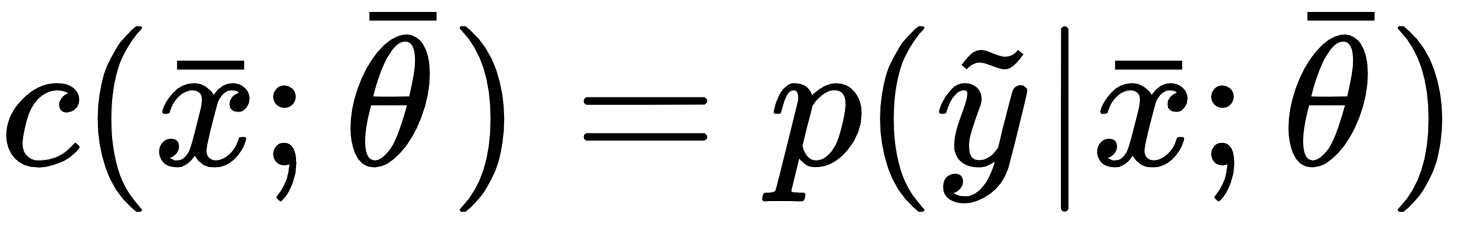
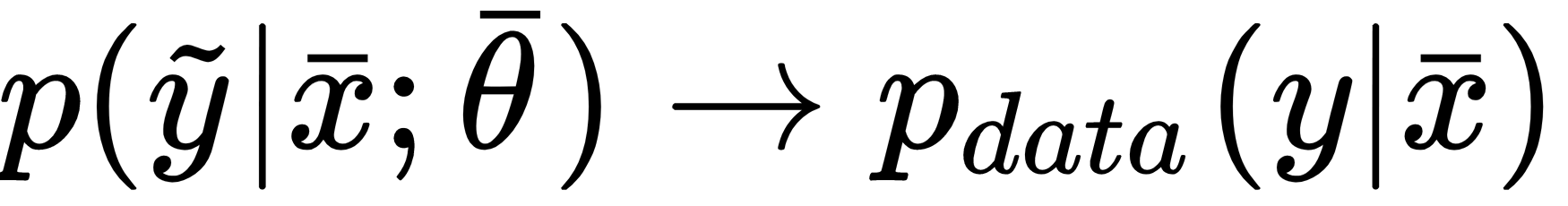
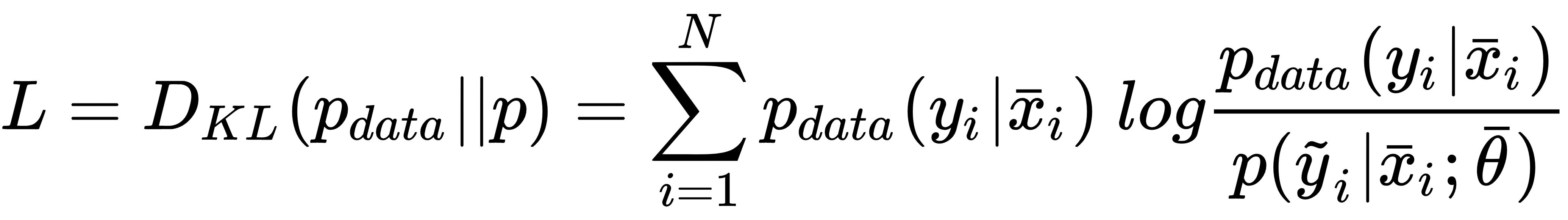
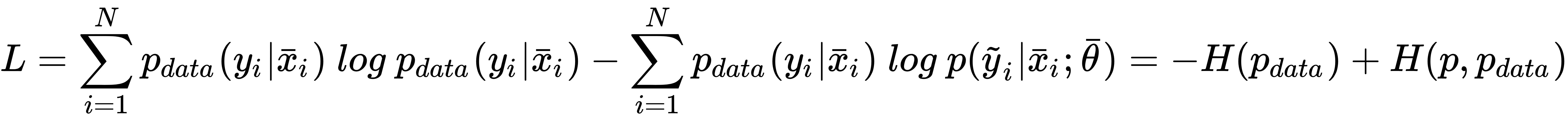
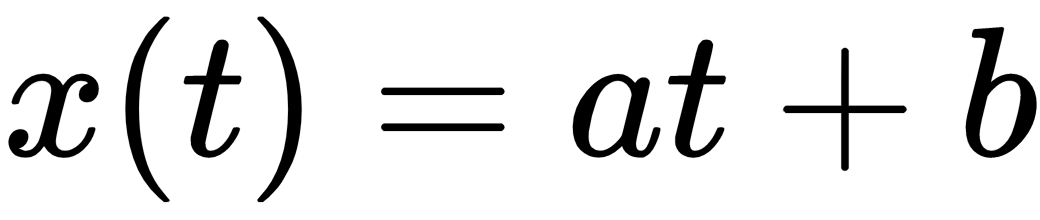
 and we define the dataset X as:
and we define the dataset X as: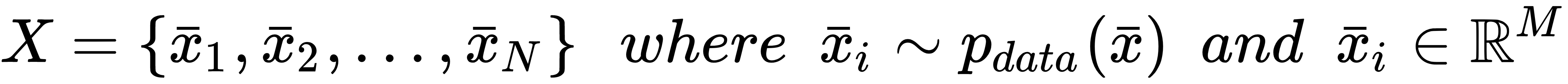
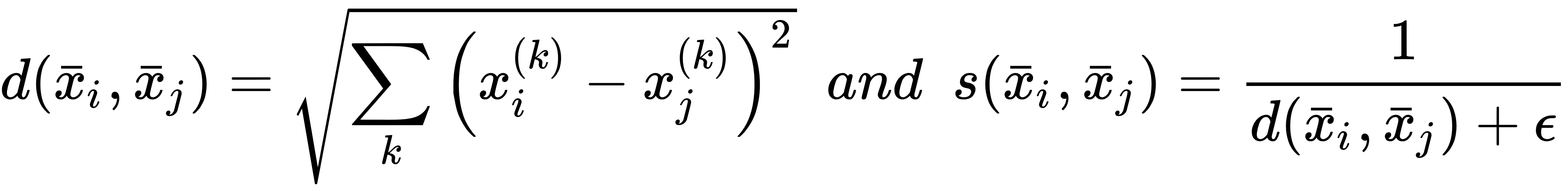
 , we can create the set of assigned vectors considering the rule:
, we can create the set of assigned vectors considering the rule: