To understand how we may be able to predict a value by using linear regression from first principles in an even better way, we need to study the gradient descent algorithm and then implement it in Python.
A gradient descent algorithm is an iterative algorithm that updates the variables in the model to fit the data, making as few errors as possible. More generally, it finds the minimum of a function.
We would like to express the weight in terms of height by using a linear formula:

We estimate the parameter,
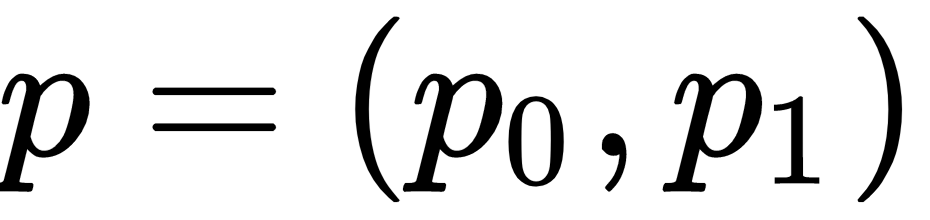
, using n data samples

to minimize the following square error:
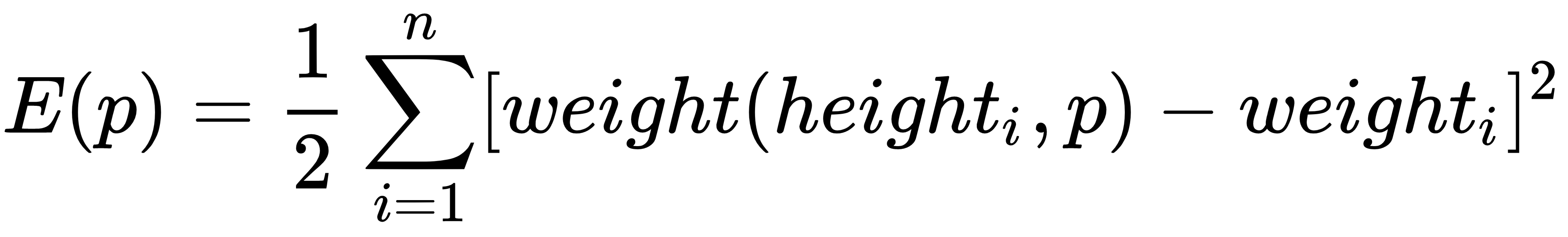
The gradient descent algorithm does this by updating the pi parameter in the direction of (∂/∂ pj) E(p), in particular:

Here, learning_rate determines that the speed of the convergence of E(p) is at the minimum. Updating the p parameter will result in the convergence of E(p) to a certain value, providing that learning_rate is sufficiently small. In the...



