Introduction to the basic terminology and notations
Now that we have discussed the three broad categories of machine learning—supervised, unsupervised, and reinforcement learning—let's have a look at the basic terminology that we will be using throughout this book. The following subsection covers the common terms we will be using when referring to different aspects of a dataset, as well as the mathematical notation to communicate more precisely and efficiently.
As machine learning is a vast field and very interdisciplinary, you are guaranteed to encounter many different terms that refer to the same concepts sooner rather than later. The second subsection collects many of the most commonly used terms that are found in machine learning literature, which may be useful to you as a reference section when reading more diverse machine learning literature.
Notation and conventions used in this book
The following table depicts an excerpt of the Iris dataset, which is a classic example in the field of machine learning. The Iris dataset contains the measurements of 150 Iris flowers from three different species—Setosa, Versicolor, and Virginica. Here, each flower example represents one row in our dataset, and the flower measurements in centimeters are stored as columns, which we also call the features of the dataset:
To keep the notation and implementation simple yet efficient, we will make use of some of the basics of linear algebra. In the following chapters, we will use a matrix and vector notation to refer to our data. We will follow the common convention to represent each example as a separate row in a feature matrix, X, where each feature is stored as a separate column.
The Iris dataset, consisting of 150 examples and four features, can then be written as a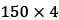 
matrix, 
:
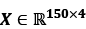Notational conventions
For the rest of this book, unless noted otherwise, we will use the superscript i to refer to the ith training example, and the subscript j to refer to the jth dimension of the training dataset.
We will use lowercase, bold-face letters to refer to vectors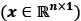 
and uppercase, bold-face letters to refer to matrices 
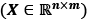. To refer to single elements in a vector or matrix, we will write the letters in italics (
or 
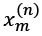, respectively).
For example,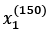 
refers to the first dimension of flower example 150, the sepal length. Thus, each row in this feature matrix represents one flower instance and can be written as a four-dimensional row vector, 
:
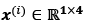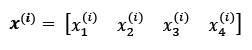
And each feature dimension is a 150-dimensional column vector, 
. For example:
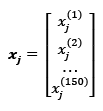
Similarly, we will store the target variables (here, class labels) as a 150-dimensional column vector:
Machine learning terminology
Machine learning is a vast field and also very interdisciplinary as it brings together many scientists from other areas of research. As it happens, many terms and concepts have been rediscovered or redefined and may already be familiar to you but appear under different names. For your convenience, in the following list, you can find a selection of commonly used terms and their synonyms that you may find useful when reading this book and machine learning literature in general:
- Training example: A row in a table representing the dataset and synonymous with an observation, record, instance, or sample (in most contexts, sample refers to a collection of training examples).
- Training: Model fitting, for parametric models similar to parameter estimation.
- Feature, abbrev. x: A column in a data table or data (design) matrix. Synonymous with predictor, variable, input, attribute, or covariate.
- Target, abbrev. y: Synonymous with outcome, output, response variable, dependent variable, (class) label, and ground truth.
- Loss function: Often used synonymously with a cost function. Sometimes the loss function is also called an error function. In some literature, the term "loss" refers to the loss measured for a single data point, and the cost is a measurement that computes the loss (average or summed) over the entire dataset.