Why graph neural networks?

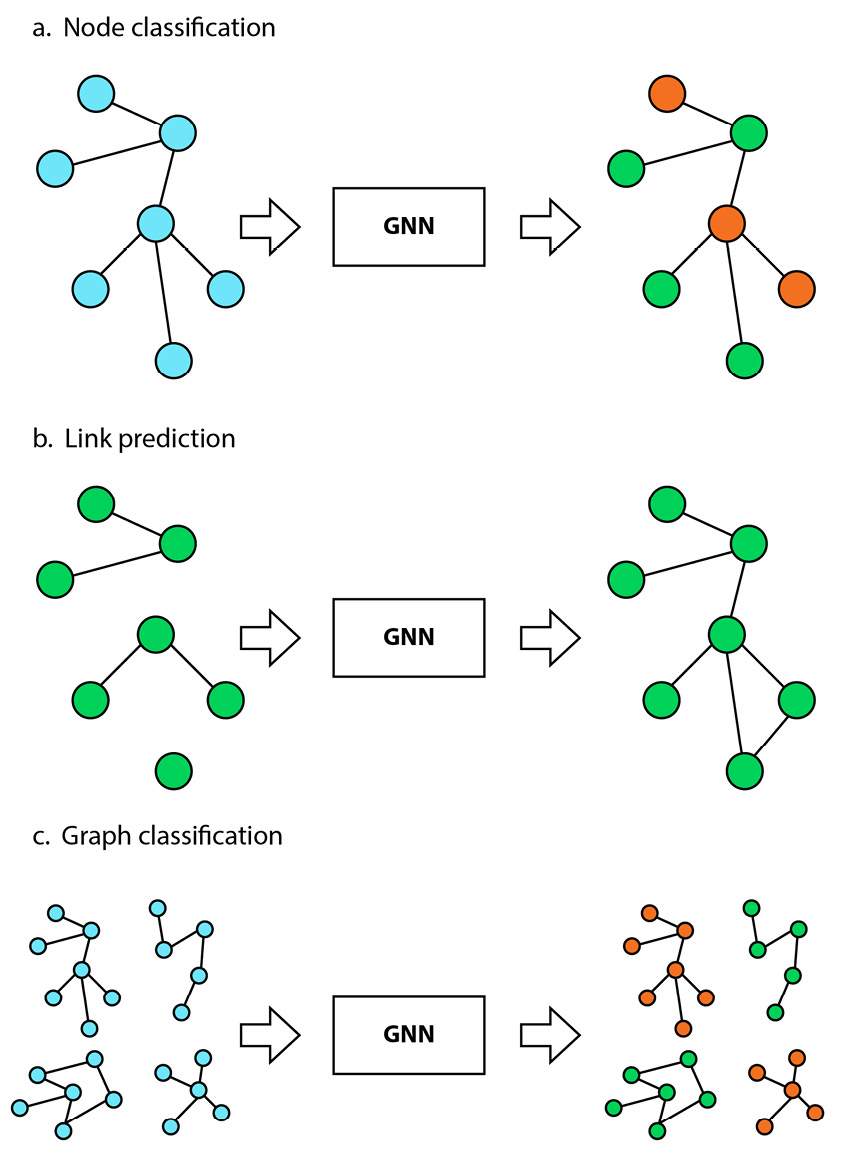
In this book, we will focus on the deep learning family of graph learning techniques, often referred to as graph neural networks. GNNs are a new category of deep learning architecture and are specifically designed for graph-structured data. Unlike traditional deep learning algorithms, which have been primarily developed for text and images, GNNs are explicitly made to process and analyze graph datasets (see Figure 1.4).

Figure 1.4 – High-level architecture of a GNN pipeline, with a graph as input and an output that corresponds to a given task

GNNs have emerged as a powerful tool for graph learning and have shown excellent results in various tasks and industries. One of the most striking examples is how a GNN model identified a new antibiotic [2]. The model was trained on 2,500 molecules and was tested on a library of 6,000 compounds. It predicted that a molecule called halicin should be able to kill many antibiotic-resistant bacteria while having low toxicity to human cells. Based on this prediction, the researchers used halicin to treat mice infected with antibiotic-resistant bacteria. They demonstrated its effectiveness and believe the model could be used to design new drugs.

How do GNNs work? Let’s take the example of a node classification task in a social network, like the previous family tree (Figure 1.3). In a node classification task, GNNs take advantage of information from different sources to create a vector representation of each node in the graph. This representation encompasses not only the original node features (such as name, age, and gender) but also information from edge features (such as the strength of relationships between nodes) and global features (such as network-wide statistics).

This is why GNNs are more efficient than traditional machine learning techniques on graphs. Instead of being limited to the original attributes, GNNs enrich the original node features with attributes from neighboring nodes, edges, and global features, making the representation much more comprehensive and meaningful. The new node representations are then used to perform a specific task, such as node classification, regression, or link prediction.

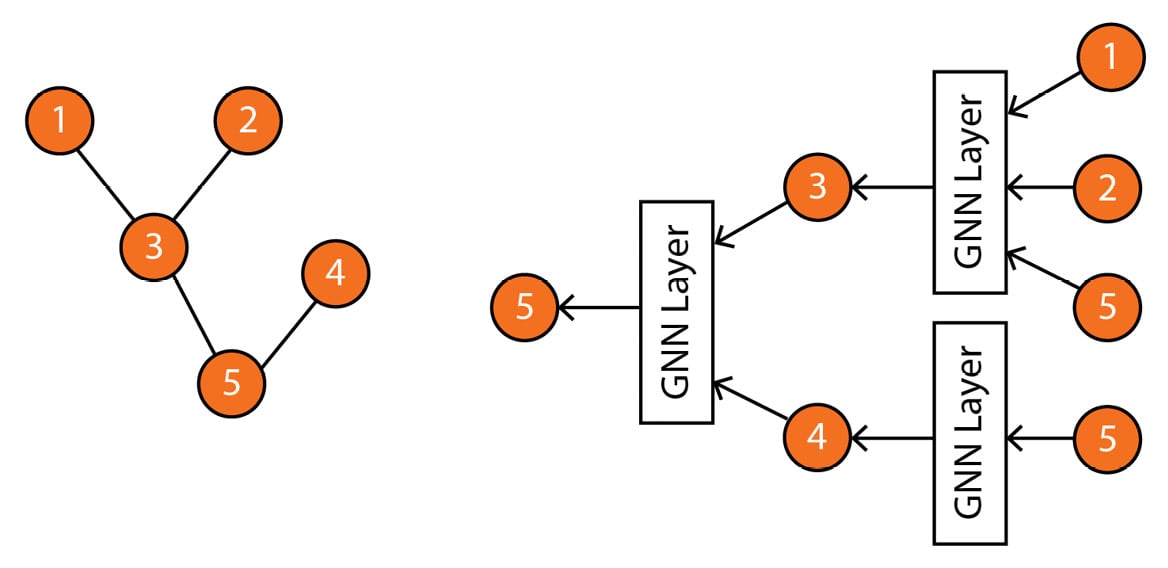
Specifically, GNNs define a graph convolution operation that aggregates information from the neighboring nodes and edges to update the node representation. This operation is performed iteratively, allowing the model to learn more complex relationships between nodes as the number of iterations increases. For example, Figure 1.5 shows how a GNN would calculate the representation of node 5 using neighboring nodes.

Figure 1.5 – Left: input graph; right: computation graph representing how a GNN computes the representation of node 5 based on its neighbors

It is worth noting that Figure 1.5 provides a simplified illustration of a computation graph. In reality, there are various kinds of GNNs and GNN layers, each of which has a unique structure and way of aggregating information from neighboring nodes. These different variants of GNNs also have their own advantages and limitations and are well-suited for specific types of graph data and tasks. When selecting the appropriate GNN architecture for a particular problem, it is crucial to understand the characteristics of the graph data and the desired outcome.

More generally, GNNs, like other deep learning techniques, are most effective when applied to specific problems. These problems are characterized by high complexity, meaning that learning good representations is critical to solving the task at hand. For example, a highly complex task could be recommending the right products among billions of options to millions of customers. On the other hand, some problems, such as finding the youngest member of our family tree, can be solved without any machine learning technique.

Furthermore, GNNs require a substantial amount of data to perform effectively. Traditional machine learning techniques might be a better fit in cases where the dataset is small, as they are less reliant on large amounts of data. However, these techniques do not scale as well as GNNs. GNNs can process bigger datasets thanks to parallel and distributed training. They can also exploit the additional information more efficiently, which produces better results.