We can thus say that any value in a time series can be represented through a function of the four components we discussed earlier—trend, seasonality, error, and cycle. The relationship between the four components can be either additive or multiplicative.
The additive model is used when the seasonal variation stays about the same across time. The trend may be upward or downward, but the seasonality stays more or less the same. A plot of such data will look very similar to this:
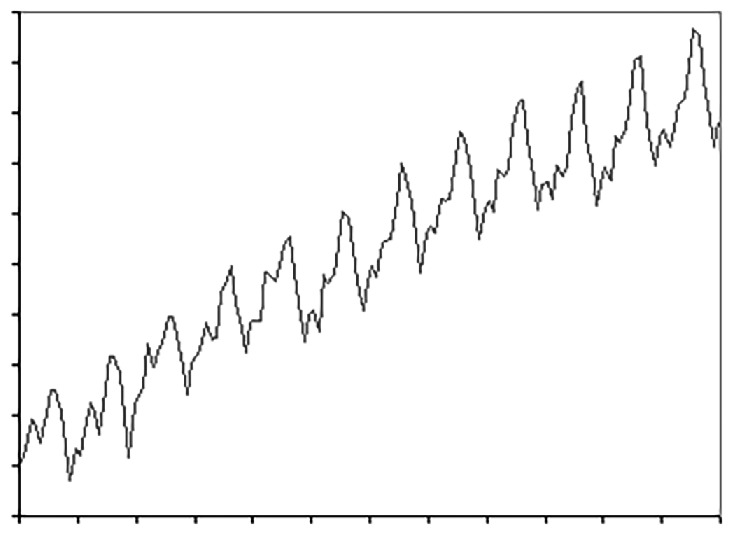
If we draw two imaginary lines between the yearly maximums and the yearly minimums, the lines will be pretty much parallel.
For an additive time series model, the four components are summed up to produce the values in the series. Thus, a time series Y can be decomposed into Y = Trend + Cycle + Seasonality + Noise.
A multiplicative model should be used with a time series where the seasonal variability increases over time. For example, a typical multiplicative time series is represented by the international...



