Overview of this book
Data structures allow organizing data efficiently. They are critical to various problems and their suitable implementation can provide a complete solution that acts like reusable code. In this book, you will learn how to use various data structures while developing in the C# language as well as how to implement some of the most common algorithms used with such data structures.
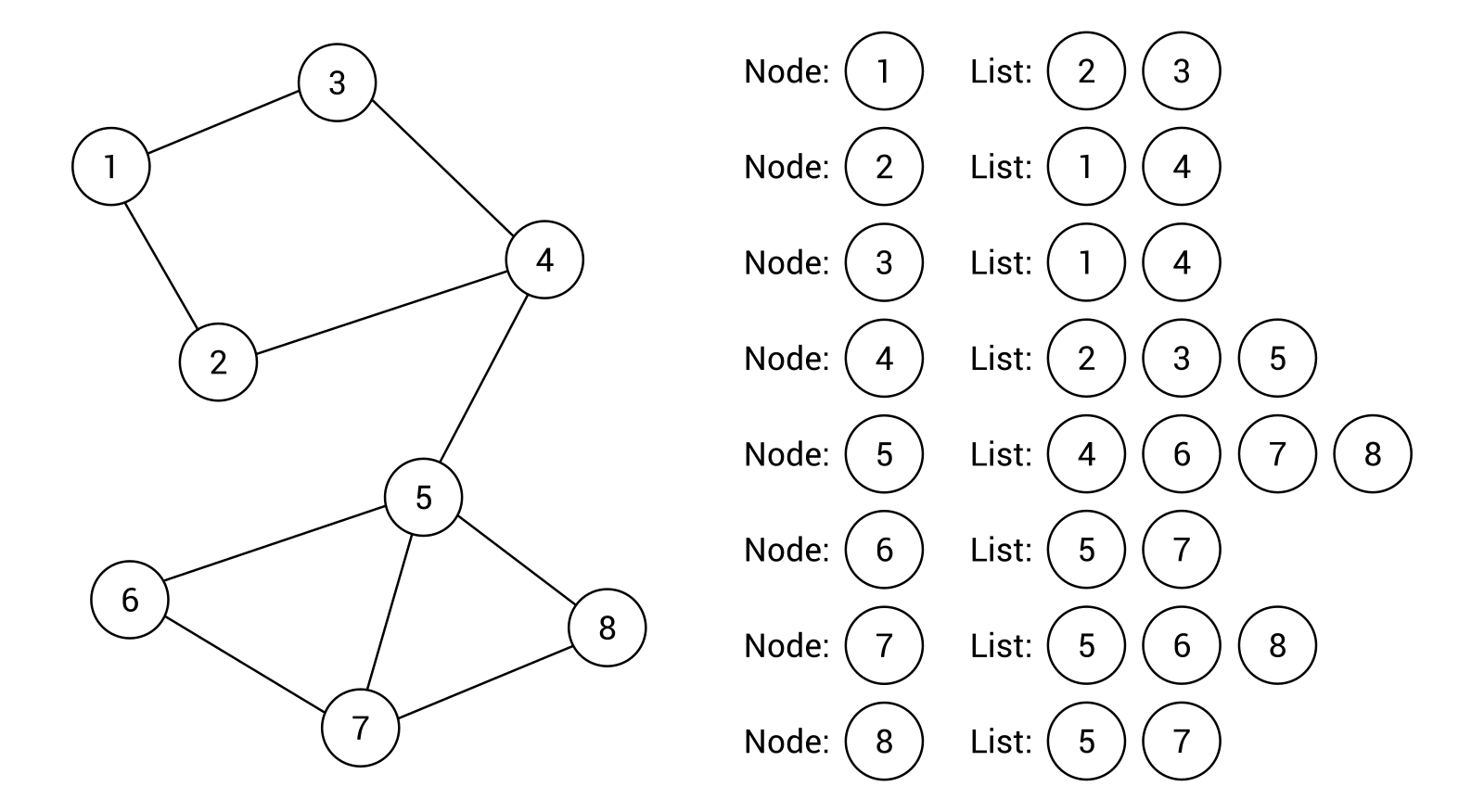
At the beginning, you will get to know arrays, lists, dictionaries, and sets together with real-world examples of your application. Then, you will learn how to create and use stacks and queues. In the following part of the book, the more complex data structures will be introduced, namely trees and graphs, together with some algorithms for searching the shortest path in a graph. We will also discuss how to organize the code in a manageable, consistent, and extendable way. By the end of the book,you will learn how to build components that are easy to understand, debug, and use in different applications.



 Free Chapter
Free Chapter