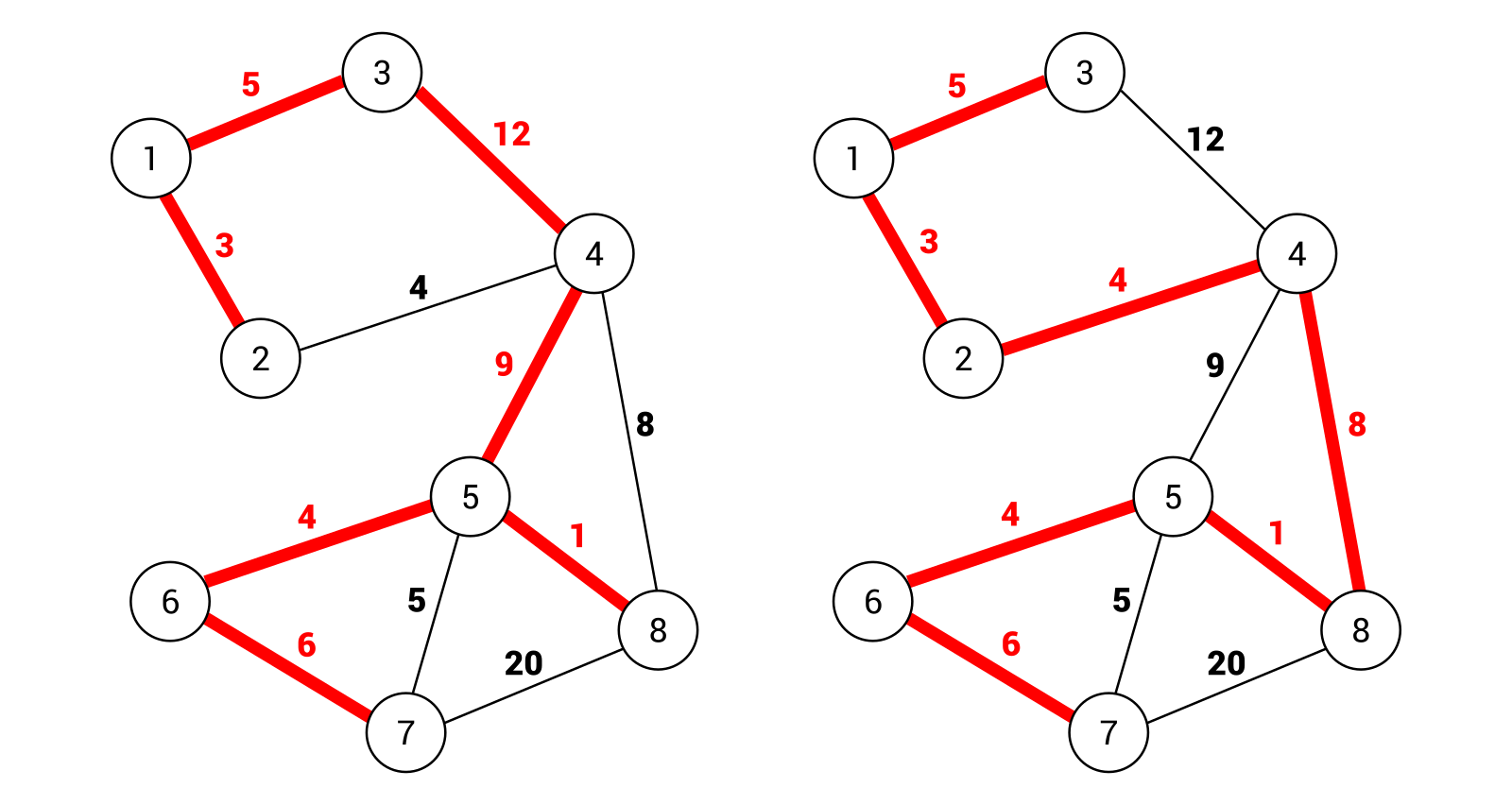
While talking about graphs, it is beneficial to introduce the subject of a spanning tree. What is it? A spanning tree is a subset of edges that connects all nodes in a graph without cycles. Of course, it is possible to have many spanning trees within the same graph. For example, let's take a look at the following diagram:
On the left-hand side is a spanning tree that consists of the following edges: (1, 2), (1, 3), (3, 4), (4, 5), (5, 6), (6, 7), and (5, 8). The total weight is equal to 40. On the right-hand side, another spanning tree is shown. Here, the following edges are taken into account: (1, 2), (1, 3), (2, 4), (4, 8), (5, 8), (5, 6), and (6, 7). The total weight is equal to 31.
However, neither of the preceding spanning trees is the minimum spanning tree (MST) of this graph. What does it mean that a spanning tree is minimum? The answer is really simple: it is a spanning tree with the minimum cost from all spanning trees available in the graph. You can get the...



 Free Chapter
Free Chapter