Heaps

In the previous chapter, we had a brief look at heaps and how C++ provides heaps via STL. In this chapter, we'll take a deeper look at heaps. Just to recap, the following are the intended time complexities:

• O(1): Immediate access to the max element
• O(log n): Insertion of any element
• O(log n): Deletion of the max element

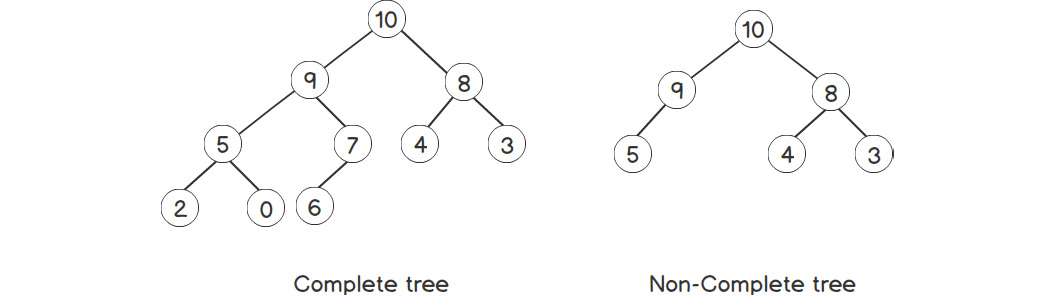
To achieve O(log n) insertion/deletion, we'll use a tree to store data. But in this case, we'll 'use a complete tree. A complete tree is defined as a tree where nodes at all the levels except the last one have two children, and the last level has as many of the elements on the left side as possible. For example, consider the two trees shown in the following figure:

Figure 2.14: Complete versus non-complete tree

Thus, a complete tree can be constructed by inserting elements in the last level, as long as there's enough space there. If not, we will insert them at the leftmost position on the new level. This gives...