Overfitting (one word) is such an important concept that I decided to start discussing it very early in the book.
If we go through many practice questions for an exam, we may start to find ways to answer questions which have nothing to do with the subject material. For instance, given only five practice questions, we find that if there are two potato and one tomato in a question, the answer is always A, if there are one potato and three tomato in a question, the answer is always B, then we conclude this is always true and apply such theory later on even though the subject or answer may not be relevant to potatoes or tomatoes. Or even worse, you may memorize the answers for each question verbatim. We can then score high on the practice questions; we do so with the hope that the questions in the actual exams will be the same as practice questions. However, in reality, we will score very low on the exam questions as it is rare that the exact same questions will occur in the actual exams.
The phenomenon of memorization can cause overfitting. We are over extracting too much information from the training sets and making our model just work well with them, which is called low bias in machine learning. However, at the same time, it will not help us generalize with data and derive patterns from them. The model as a result will perform poorly on datasets that were not seen before. We call this situation high variance in machine learning.
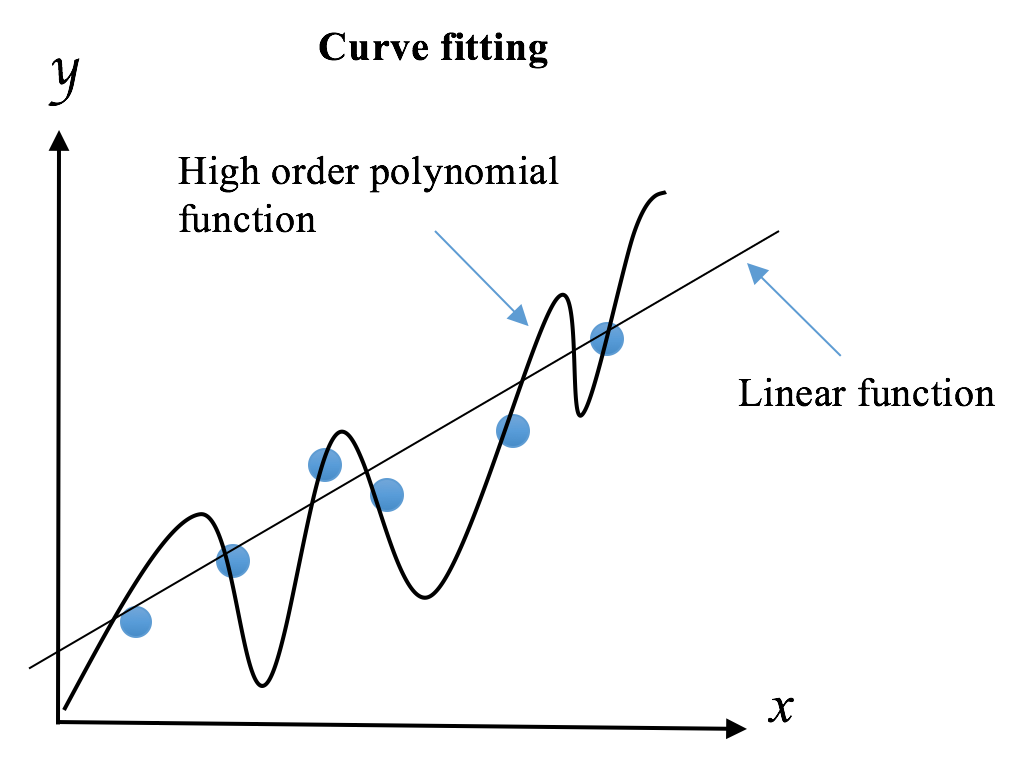
Overfitting occurs when we try to describe the learning rules based on a relatively small number of observations, instead of the underlying relationship, such the preceding potato and tomato example. Overfitting also takes place when we make the model excessively complex so that it fits every training sample, such as memorizing the answers for all questions as mentioned previously.
The opposite scenario is called underfitting. When a model is underfit, it does not perform well on the training sets, and will not so on the testing sets, which means it fails to capture the underlying trend of the data. Underfitting may occur if we are not using enough data to train the model, just like we will fail the exam if we did not review enough material; it may also happen if we are trying to fit a wrong model to the data, just like we will score low in any exercises or exams if we take the wrong approach and learn it the wrong way. We call any of these situations high bias in machine learning, although its variance is low as performance in training and test sets are pretty consistent, in a bad way.
We want to avoid both overfitting and underfitting. Recall bias is the error stemming from incorrect assumptions in the learning algorithm; high bias results in underfitting, and variance measures how sensitive the model prediction is to variations in the datasets. Hence, we need to avoid cases where any of bias or variance is getting high. So, does it mean we should always make both bias and variance as low as possible? The answer is yes, if we can. But in practice, there is an explicit trade-off between themselves, where decreasing one increases the other. This is the so-called bias–variance tradeoff. Does it sound abstract? Let’s take a look at the following example.
We were asked to build a model to predict the probability of a candidate being the next president based on the phone poll data. The poll was conducted by zip codes. We randomly choose samples from one zip code, and from these, we estimate that there's a 61% chance the candidate will win. However, it turns out he loses the election. Where did our model go wrong? The first thing we think of is the small size of samples from only one zip code. It is the source of high bias, also because people in a geographic area tend to share similar demographics. However, it results in a low variance of estimates. So, can we fix it simply by using samples from a large number zip codes? Yes, but don’t get happy so early. This might cause an increased variance of estimates at the same time. We need to find the optimal sample size, the best number of zip codes to achieve the lowest overall bias and variance.
Minimizing the total error of a model requires a careful balancing of bias and variance. Given a set of training samples x_1, x_2, …, x_n and their targets y_1, y_2, …, y_n, we want to find a regression function, ŷ(x), which estimates the true relation y(x) as correctly as possible. We measure the error of estimation, how good (or bad) the regression model is by mean squared error (MSE):
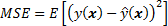
The E denotes the expectation. This error can be decomposed into bias and variance components following the analytical derivation as follows (although it requires a bit of basic probability theory to understand):
![]()
![]()
![]()
![]()
![]()
![]()
The bias term measures the error of estimations, and the variance term describes how much the estimation ŷ moves around its mean. The more complex the learning model ŷ(x) and the larger the size of training samples, the lower the bias will be. However, these will also create more shift on the model in order to fit better the increased data points. As a result, the variance will be lifted.
We usually employ the cross-validation technique to find the optimal model balancing bias and variance and to diminish overfitting.
The last term is the irreducible error.