There are many continuous action space algorithms in deep reinforcement learning topology. Some of them, which we covered earlier in Chapter 4, Policy Gradients, were mainly stochastic policy gradients and stochastic actor-critic algorithms. Stochastic policy gradients were associated with many problems such as difficulty in choosing step size owing to the non-stationary data due to continuous change in observation and reward distribution, where a bad step would adversely affect the learning of the policy network parameters. Therefore, there was a need for an approach that can restrict this policy search space and avoid bad steps while training the policy network parameters.
Here, we will try to cover some of the advanced continuous action space algorithms:
- Trust region policy optimization
- Deterministic policy gradients
Trustregion policy optimization (TRPO) is an iterative approach for optimizing policies. TRPO optimizes large nonlinear policies. TRPO restricts the policy search space by applying constraints on the output policy distributions. In order to do this, KL divergence loss function (
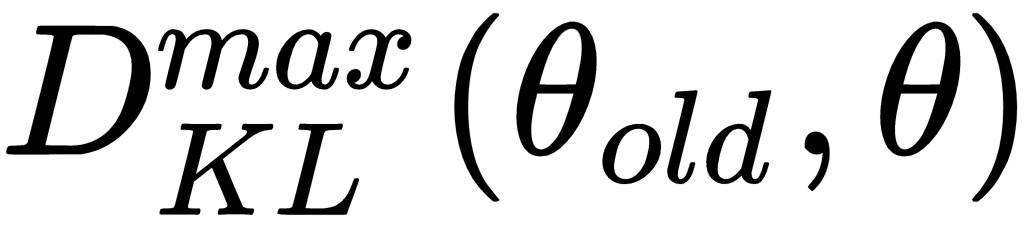
) is used on the policy network parameters to penalize these parameters. This KL divergence constraint between the new and the old policy is called the trust region constraint. As a result of this constraint large scale changes don't occur in the policy distribution, thereby resulting in early convergence of the policy network.
TRPO was published by Schulman et. al. 2017 in the research publication named Trust Region Policy Optimization (https://arxiv.org/pdf/1502.05477.pdf). Here they have mention the experiments demonstrating the robust performance of TRPO on different tasks such as learning simulated robotic swimming, playing Atari games, and many more. In order to study TRPO in detail, please follow the arXiv link of the publication: https://arxiv.org/pdf/1502.05477.pdf.
Deterministic policy gradients was proposed by Silver et. al. in the publication named Deterministic Policy Gradient Algorithms (http://proceedings.mlr.press/v32/silver14.pdf). In continuous action spaces, policy improvement with greedy approach becomes difficult and requires global optimization. Therefore, it is better and tractable to update the policy network parameters in the direction of the gradient of the Q function, as follows:
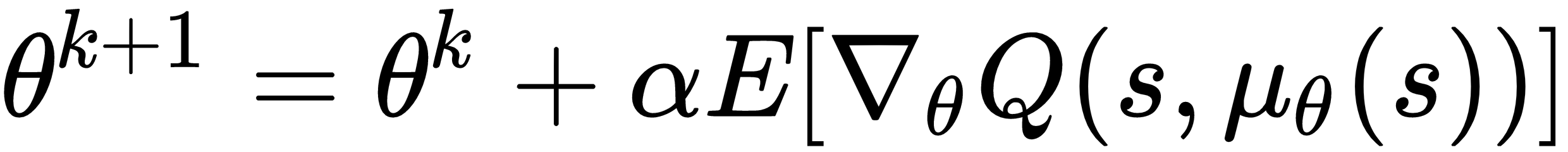
where,
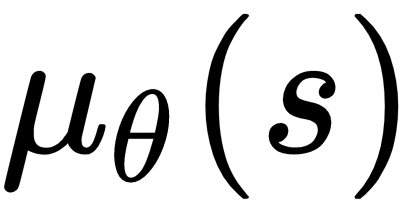
is the deterministic policy, α is the learning rate and θ representing the policy network parameters. By applying the chain rule, the policy improvement can be shown as follows:
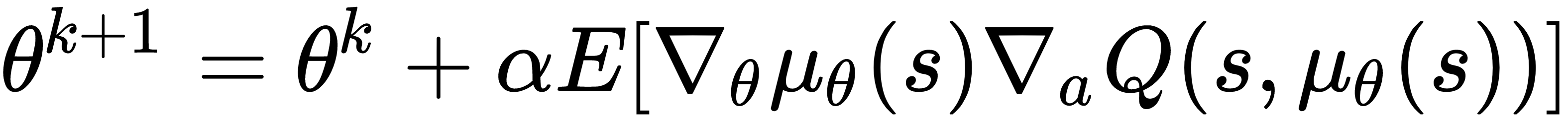
The preceding update rule can be incorporated into a policy networks where the parameters are updated using stochastic gradient ascent. This can be realized as a deterministic actor-critic method where the critic estimates the action-value function while the actor derives its gradients from the critic to update its parameters. As mentioned in Deterministic Policy Gradient Algorithms (http://proceedings.mlr.press/v32/silver14.pdf) by Silver et. al., post experimentation, they were able to successfully conclude that the deterministic policy gradients are more efficient than their stochastic counterparts. Moreover, deterministic actor-critic outperformed its stochastic counterpart by a significant margin. A detailed explanation of this topic is out of the scope of this book. So please go to the research publication link mentioned previously.



