Hill climbing and descent
We will go back to our example—the lost hill that we looked at. We want to find a way to select a set of theta parameters that is going to minimize our loss function, L. As we've already established, we need to climb or descend the hill, and understand where we are with respect to our neighboring points without having to compute everything. To do that, we need to be able to measure the slope of the curve with respect to the theta parameters. So, going back to our house example, as mentioned before, we want to know how much correct the incremental value of cost per square foot makes. Once we know that, we can start taking directional steps toward finding the best estimate. So, if you make a bad guess, you can turn around and go in exactly the other direction. So, we can either climb or descend the hill depending on our metric, which allows us to optimize the parameters of a function that we want to learn irrespective of how the function itself performs. This is a layer of abstraction. This optimization process is called gradient descent, and it supports many of the machine learning algorithms that we will discuss in this book.
The following code shows a simple example of how we can measure the gradient of a matrix with respect to theta. This example is actually a simplified snippet of the learning component of logistic regression:
import numpy as np
seed = (42)
X = np.random.RandomState(seed).rand(5, 3).round(4)
y = np.array([1, 1, 0, 1, 0])
h = (lambda X: 1. / (1. + np.exp(-X)))
theta = np.zeros(3)
lam = 0.05
def iteration(theta):
y_hat = h(X.dot(theta))
residuals = y - y_hat
gradient = X.T.dot(residuals)
theta += gradient * lam
print("y hat: %r" % y_hat.round(3).tolist())
print("Gradient: %r" % gradient.round(3).tolist())
print("New theta: %r\n" % theta.round(3).tolist())
iteration(theta)
iteration(theta)At the very top, we randomly initialize X and y, which is not part of the algorithm. So, x here is the sigmoid function, also called the logistic function. The word logistic comes from logistic progression. This is a necessary transformation that is applied in logistic regression. Just understand that we have to apply that; it's part of the function. So, we initialize our theta vector, with respect to which we're going to compute our gradient as zeros. Again, all of them are zeros. Those are our parameters. Now, for each iteration, we're going to get our
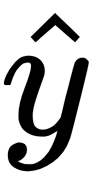
, which is our estimated y, if you recall. We get that by taking the dot product of our X matrix against our theta parameters, pushed through that logistic function, h, which is our
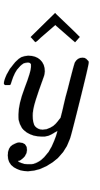
.
Now, we want to compute the gradient of that dot product between the residuals and the input matrix, X, of our predictors. The way we compute our residuals is simply y minus
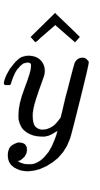
, which gives the residuals. Now, we have our
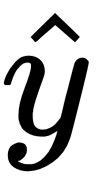
. How do we get the gradient? The gradient is just the dot product between the input matrix, X, and those residuals. We will use that gradient to determine which direction we need to step in. The way we do that is we add the gradient to our theta vector. Lambda regulates how quickly we step up or down that gradient. So, it's our learning rate. If you think of it as a step size—going back to that dark room example—if it's too large, it's easy to overstep the lowest point. But if it's too small, you're going to spend forever inching around the room. So, it's a bit of a balancing act, but it allows us to regulate the pace at which we update our theta values and descend our gradient. Again, this algorithm is something we will cover in the next chapter.
We get the output of the preceding code as follows:
y hat: [0.5, 0.5, 0.5, 0.5, 0.5] Gradient: [0.395, 0.024, 0.538] New theta: [0.02, 0.001, 0.027] y hat: [0.507, 0.504, 0.505, 0.51, 0.505] Gradient: [0.378, 0.012, 0.518] New theta: [0.039, 0.002, 0.053]
This example demonstrates how our gradient or slope actually changes as we adjust our coefficients and vice versa.
In the next section, we will see how to evaluate our models and learn the cryptic train_test_split.



