Elementary set theory
In mathematics, set theory is the study of collections of objects, which is prerequisite knowledge for studying discrete mathematics.
Definition–Sets and set notation
A set is a collection of objects. If a set A is made up of objects a1, a2, …, we write it as A = {a1, a2, …}.
Definition: Elements of sets
Each object in a set A is called an element of A, and we write an  A.
A.
Definition: The empty set
Sets may contain many sorts of objects—numbers, points, vectors, functions, or even other sets.
Example: Some examples of sets
Examples of sets include the following:
- The set of prime numbers less than 10 is A = {2, 3, 5, 7}.
- The set of the three largest cities in the world is {Tokyo, Delhi, Shanghai}.
- The natural numbers are a set N = {1, 2, 3, …}.
- The integers are a set Z = {…, -3, -2, -1, 0, 1, 2, 3, …}.
- If B, C, and D are sets, A = {B, C, D} is a set of sets.
- The real numbers are written R = (-∞, ∞), which consists of the entire number line. Note that it is not possible to list the real numbers within braces, as we can with N or Z.
Definition: Subsets and supersets
A set A is a subset of B if all elements in A are also in B, and we write it as A  B. We call B a superset of A. If A is a subset of B, but they are not the same set, we call A a proper subset of B, and write A
B. We call B a superset of A. If A is a subset of B, but they are not the same set, we call A a proper subset of B, and write A  B.
B.
It is helpful to have an alternative notation in order to construct sets satisfying certain criteria, which we call set-builder notation, defined next.
Definition: Set-builder notation
A set may be written as {x  A | Conditions}, which consists of the subset of A such that the given conditions are true.
A | Conditions}, which consists of the subset of A such that the given conditions are true.
Sometimes, sets will be expressed as {x | Conditions} when it is obvious what kind of mathematical object x is from the context.
Example: Using set-builder notation
Examples of sets constructed by set-builder notation include the following.
- The set of even natural numbers is {2, 4, 6, ...} = {n | n = 2k for some k
 N}. This is an infinite set where each element n is 2 * k, where k is some natural number belonging to the set {1, 2, 3…..}.
N}. This is an infinite set where each element n is 2 * k, where k is some natural number belonging to the set {1, 2, 3…..}. - The closed interval of real numbers from a to b is {x
 R | a ≤ x ≤ b} = [a, b].
R | a ≤ x ≤ b} = [a, b]. - The open interval of real numbers from a to b is {x
 R | a < x < b} = (a, b).
R | a < x < b} = (a, b). - The set R2 = {(x, y) | x, y
 R} consists of the entire 2D coordinate plane.
R} consists of the entire 2D coordinate plane. - The line with slope 2 and y-intercept 3 is the set {(x, y)
 R2 | y = 2x + 3}.
R2 | y = 2x + 3}. - The open ball of radius r and center (0, 0) is {(x, y)
 R2 | x2 + y2 < r}, which is the interior, but not the boundary of a circle.
R2 | x2 + y2 < r}, which is the interior, but not the boundary of a circle. - A circle of radius r and center (0, 0) is {(x, y)
 R2 | x2 + y2 = r}, which is the boundary of the circle.
R2 | x2 + y2 = r}, which is the boundary of the circle. - The set of all African nations is {x
 Nations | x is in Africa}.
Nations | x is in Africa}.
There are some useful operations that may be done to pairs of sets, which we will see in the next definition.
Definition: Basic set operations
Let A and B be sets. Let's take a look at the basic operations:
- The union of sets A and B is the set of all elements in A or B (or both) and is denoted A
 B = {x | x
B = {x | x  A or x
A or x  B}.
B}. - A union of sets A1, A2, … is denoted
 .
. - The intersection of sets A and B is the set of all elements in both A and B. It is denoted A
 B = {x | x
B = {x | x  A and x
A and x  B}.
B}. - An intersection of sets A1, A2, … is denoted
 .
. - The complement of set A is all elements in the set that are not in A and is denoted AC = {x | x
 A}.
A}. - The difference between sets A and B is the set of all elements in A, but not B, denoted A - B = {x
 A | x
A | x  B}.
B}.
It is often useful to represent these set operations with Venn diagrams, which are visual displays of sets. Here are some examples of the operations shown previously:
- The following displays A
 B:
B:
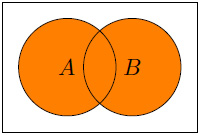
Figure 1.3 – A  B
B
- The following displays A
 B:
B:
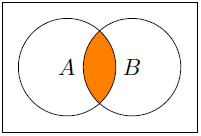
Figure 1.4 – A  B
B
- The following displays Ac:
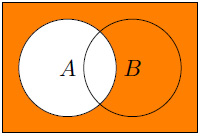
Figure 1.5 – Ac
- The following displays A – B:
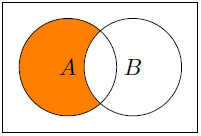
Figure 1.6 – A - B
As an example, consider the following diagram. We can use the language of set theory to describe many aspects of the diagram:
- Elements a, b, and d are in set A, which we can write as a, b, d
 A.
A. - Elements c and d are in set B, and c, d
 B.
B. - Element c is not in A, so we could write c
 A or c
A or c  AC.
AC. - Element d is in both A and B, or d
 A
A  B.
B. - All four elements are in A or B (or both), so we could say a, b, c, d
 A
A  B:
B:
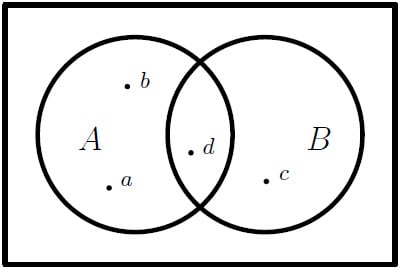
Figure 1.7 – Two sets with some elements
Definition: Disjoint sets
Sets A and B are disjoint (or mutually exclusive) if A  B =
B =  . In other words, the sets share no elements in common.
. In other words, the sets share no elements in common.
Example: Even and odd numbers
Consider sets of even natural numbers E = {2, 4, 6, ...} and odd natural numbers O = {1, 3, 5, ...}. These sets are disjoint, E  O =
O =  , since no number is both odd and even.
, since no number is both odd and even.
- E is a subset of the natural numbers, E
 N.
N. - O is a subset of the natural numbers, O
 N.
N.
The union of E and O make up the set of all-natural numbers, E  O = N.
O = N.
Theorem: De Morgan's laws
De Morgan's laws state how mathematical concepts are related through their opposites. In set theory, these laws make use of complements to address the intersection and union of sets.
De Morgan's laws can be written as follows:
- (A
 B)C = AC
B)C = AC  BC
BC - (A
 B)C = AC
B)C = AC  BC
BC
The following diagrams display De Morgan's laws:
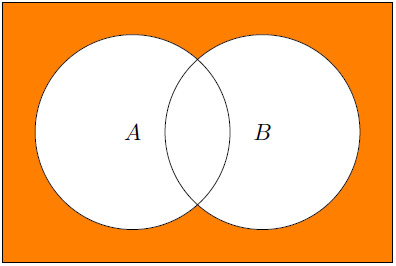
Figure 1.8 – De Morgan's laws (A  B)C = AC
B)C = AC  BC
BC
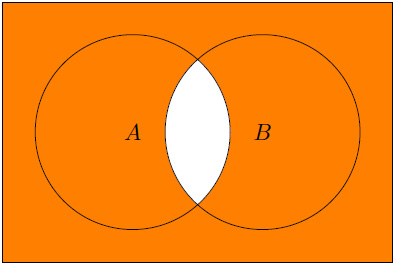
Figure 1.9 – De Morgan's laws (A  B)C = AC
B)C = AC  BC
BC
Proof:
Let's now look at the proof of this theorem:
Let x  (A
(A  B)C, then x
B)C, then x  (A
(A  B), which means x
B), which means x  A and x
A and x  B, or x
B, or x  AC and x
AC and x  BC, or x
BC, or x  AC
AC  BC. Thus, (A
BC. Thus, (A  B)C is a subset of AC
B)C is a subset of AC  BC.
BC.
Next, let x  (AC
(AC  BC), then x
BC), then x  AC and x
AC and x  BC, or x
BC, or x  A and x
A and x  B, then x
B, then x  (A
(A  B) or x
B) or x  (A
(A  B)C. Like the last step, we see AC
B)C. Like the last step, we see AC  BC is a subset of (A
BC is a subset of (A  B)C. Since (A
B)C. Since (A  B)C is a subset of AC
B)C is a subset of AC  BC and vice versa, (A
BC and vice versa, (A  B)C = AC
B)C = AC  BC.
BC.
The proof of this result is similar and is left as an exercise for the reader.
Notice that the preceding method of proof is designed to show that any element of (A  B)C is an element of AC
B)C is an element of AC  BC, and to show that any element of AC
BC, and to show that any element of AC  BC is an element of (A
BC is an element of (A  B)C, which establishes that the two sets are the same.
B)C, which establishes that the two sets are the same.
Example: De Morgan's Law
Consider two sets of natural numbers, the even numbers E = {2, 4, 6, …} and A = {1, 2, 3, 4}. If we take the set of elements in either set, or the complement of the union of the sets, we have (E  A)C = {1, 2, 3, 4, 6, 8, 10, …}C = {5, 7, 9, …}.
A)C = {1, 2, 3, 4, 6, 8, 10, …}C = {5, 7, 9, …}.
De Morgan's law states that the intersection of the complements of the sets should be equal to this. Let's verify that this is true. The complements of the sets are EC = {1, 3, 5, …} and AC = {5, 6, 7, …}. The intersection of these complements is EC  AC = {5, 7, 9, …}.
AC = {5, 7, 9, …}.
Definition: Cardinality
The cardinality, or size, of a set A is the number of elements in the set and is denoted |A|.
Example: Cardinality
The cardinalities of some sets are computed here:
- If A = {0, 1}, then of course its cardinality is |A| = 2, since there are two elements in the set.
- The cardinality of the set B = {x
 N | x < 10} is less obvious, but we can write B more explicitly. It is the set of natural numbers less than 10, so B = {1, 2, 3, 4, 5, 6, 7, 8, 9} and, clearly, |B| = 9.
N | x < 10} is less obvious, but we can write B more explicitly. It is the set of natural numbers less than 10, so B = {1, 2, 3, 4, 5, 6, 7, 8, 9} and, clearly, |B| = 9. - For the set of odd natural numbers, O = {1, 3, 5, ...}, we have an infinite cardinality, |O| = ∞, as this sequence goes on forever.
With our knowledge of set theory, we can now move on to learn about relations between different sets and functions, which help us to map each element from a set to exactly one element in another set.



