In the example of Rocket Through, the game that we developed in Chapter 5, On the Line – Rocket Through, we used vectors to describe movement, and now I want to show you the logic behind some of the methods in Cocos2d-x that we used to handle vector operations, and what do they mean.
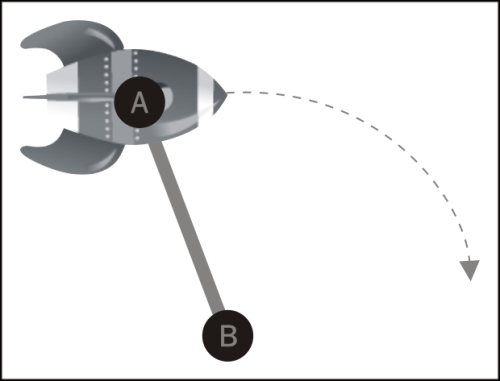
Let's start, as an example, with the rocket sprite moving with a vector of (5, 0).
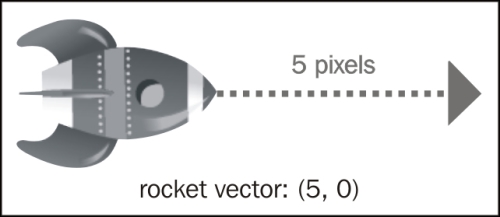
We then draw a line from the rocket, say from point A, to a point B.
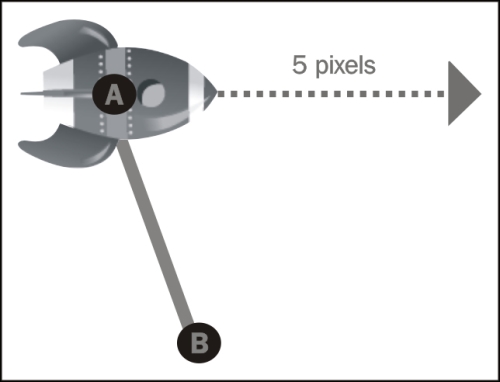
Now we want the rocket to rotate around point B. So how can we change the rocket's vector to accomplish that? With Cocos2d-x, we can use the helper point method ccpRotateByAngle to rotate a point around any other point. In this case we rotate the rocket's position point around point B by a certain angle.
But here's a question, in which direction should the rocket rotate?
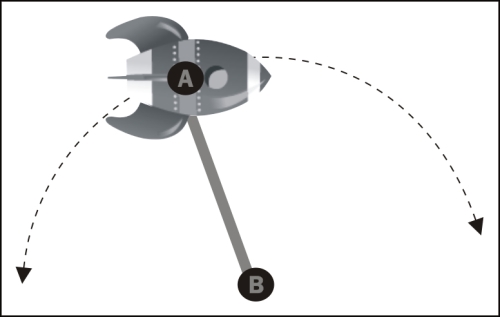
By looking at the previous figure, you know that the rocket should rotate clockwise, since it's moving towards the right. But programmatically how could we determine that and in the easiest way possible? We can determine this by using vectors and another property derived from them: the dot product.
The dot product of two vectors describe their angular relationship. If their dot product is greater than zero, the two vectors form an angle smaller than 90 degrees. If it is less than zero, the angle is greater than 90 degrees, and if it is equal to zero, the vectors are perpendicular.
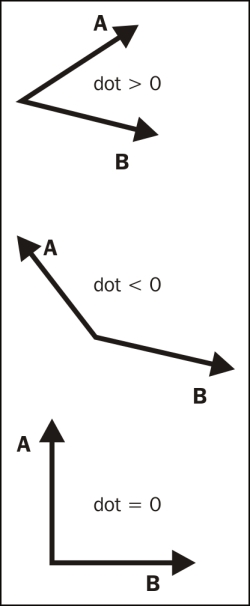
One other way to think about this is: if the dot product is a positive value, the vectors "point" to the same direction. If it is a negative value, they point to opposite directions. How can we use that to help us?
A vector will always have two perpendiculars, as shown in the following figure:
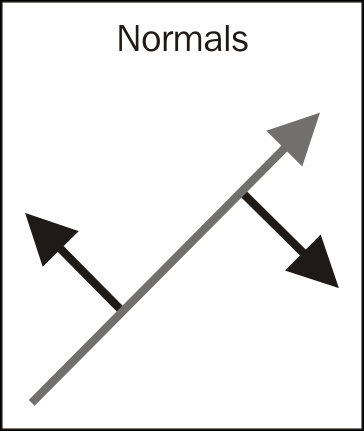
These perpendiculars are often called right and left, or clockwise and counterclockwise perpendiculars, and they are themselves vectors, known as normals.
Now if we calculate the dot product between the rocket's vector and each of the perpendiculars on line AB, you can see that we can determine the direction in which the rocket should rotate. If the dot product of the rocket and the vector's right perpendicular is a positive value, it means the rocket is moving towards the right (clockwise). If not, it means the rocket is moving towards the left (counterclockwise).
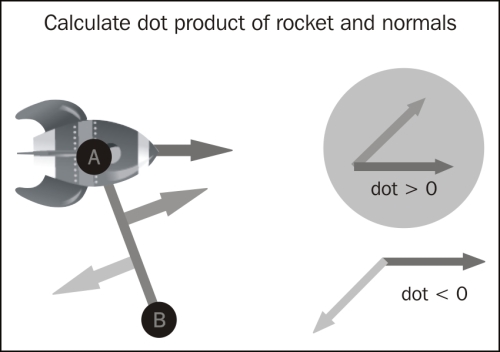
The dot product is very easy to calculate. We don't even need to bother with the formula, though it's a simple one, because we can use the ccDot(vector1, vector2) method.
So we have the
vector for the rocket already. How do we get the vector for the normals? First we get the vector for the AB line. We use another method for this ccpSub(point1, point2); this will subtract points A and B and return a vector representing that line.
Next, we can get the left and right perpendiculars of that line vector with the ccpPerp(vector) and ccpRPerp(vector) methods respectively. But we only need to check one of these. Then we get the dot product by using ccpDot(rocketVector, lineNormal).
If this is the correct normal, meaning the value for the dot product is a positive one, we can rotate the rocket to point to this normal's direction; so the rocket will be at a 90 degree angle with the line at all times as it rotates. This is easy, because we can convert the normal vector to an angle by using the ccpToAngle(vector) method. All we need to do is apply that angle to the rocket.
But how fast should the rocket rotate? We'll see how to calculate that next.
When rotating the rocket, we still want to show it moving at the same speed as it was when moving on a straight line, or as close to it as possible. How do we do that?
Remember that the vector is being used to update the rocket's position in every iteration. In the example I gave you, the (5,0) vector is currently adding 5 pixels to the x position of the rocket in every iteration.
Now let's consider an angular speed. If the angular speed were 15 degrees, and we kept rotating the rocket's position by that angle, it would mean the rocket would complete a full circle in 24 iterations, because 360 degrees of a full circle divided by 15 degrees equals 24.
But we don't have the correct angle yet, we only have the amount in pixels the rocket moves in every iteration. But math can tell us a lot here.
Math says that the length of a circle is twice the value of Pi, multiplied by the radius of the circle, usually written as 2πr.
We know the radius of the circle that we want the rocket to describe: it is the length of the line we drew.
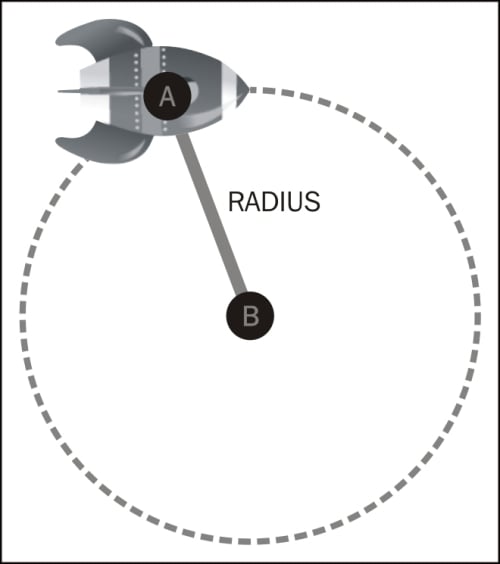
With that formula we can get the length in pixels of that circle, also known as its circumference. Let's say the line has a length of 100 pixels; this would mean the circle about to be described by the rocket has a length (or circumference) of 628.3 pixels (2 * π * 100).
With the speed described in the vector (5,0), we can determine how long it would take the rocket to complete that pixel length. We don't need this to be absolutely precise (the last iteration will most likely move beyond that total length) but it's good enough for our purposes.
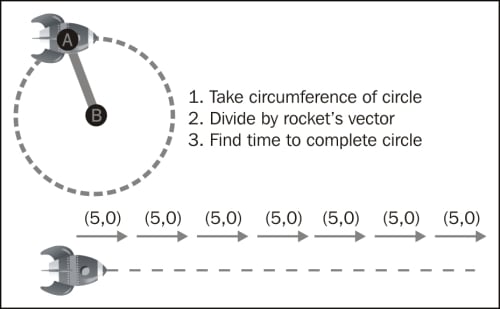
When we have the total number of iterations to complete the length, we can convert that to an angle. So if the iteration value is 125, the angle would be 360 degrees divided by 125, that is 2.88. This is the angle required to describe a circle in 125 iterations.
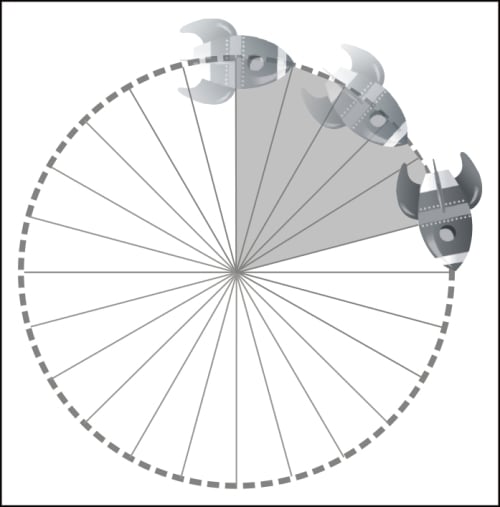
Now the rocket can change from a pixel-based movement to an angular-based movement without much visual change.



