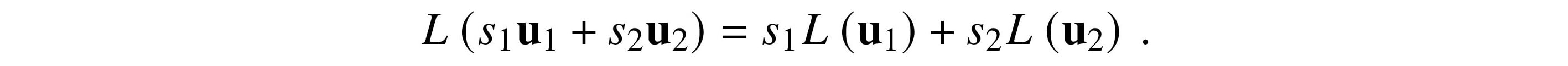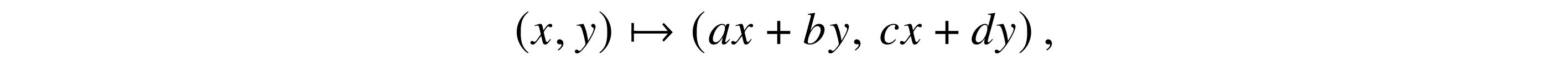Overview of this book
Dancing with Qubits, Second Edition, is a comprehensive quantum computing textbook that starts with an overview of why quantum computing is so different from classical computing and describes several industry use cases where it can have a major impact. A full description of classical computing and the mathematical underpinnings of quantum computing follows, helping you better understand concepts such as superposition, entanglement, and interference. Next up are circuits and algorithms, both basic and sophisticated, as well as a survey of the physics and engineering ideas behind how quantum computing hardware is built. Finally, the book looks to the future and gives you guidance on understanding how further developments may affect you.
This new edition is updated throughout with more than 100 new exercises and includes new chapters on NISQ algorithms and quantum machine learning.
Understanding quantum computing requires a lot of math, and this book doesn't shy away from the necessary math concepts you'll need. Each topic is explained thoroughly and with helpful examples, leaving you with a solid foundation of knowledge in quantum computing that will help you pursue and leverage quantum-led technologies.



 Free Chapter
Free Chapter