Use the following problems to test your mathematical programming prowess. I strongly encourage you to give each problem a try before you turn to the solutions and download the example programs.
Create a StatisticsExtensions class that defines extension methods to calculate statistical functions for arrays or lists of numbers. LINQ provides the Average, Max, and Min extension methods to calculate some statistical functions, so you don't need to implement those.
The following list summarizes the statistical functions that you should provide:
- Truncated mean: This is the mean (average) after removing an indicated number or percentage of the largest and smallest values. For example, if the values are {1, 1, 3, 5, 7, 7, 9} and you want to remove the two largest and smallest values, the remaining values are {3, 5, 7}.
- Median: This is the middlemost value. For example, if the values are {1, 1, 3, 5, 7, 7, 9}, then the median is 5 because half of the values are less than 5 and half are greater. If the set includes an even number of values, the median is the average of the two middlemost values.
- Mode: This is the value that occurs most often. In the set {1, 2, 3, 3, 7}, the mode is 3 because it appears twice. If there's a tie, return all of the modes in a list.
- Sample standard deviation: This is a measure of how widely spread the values are. The sample standard deviation is defined bythefollowing formula:
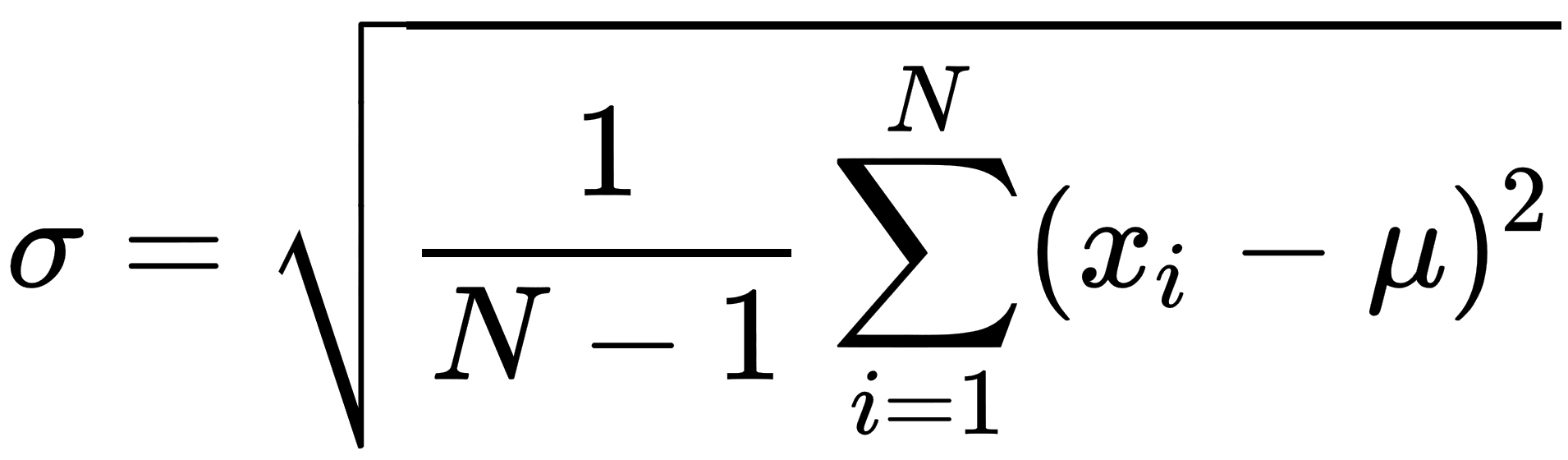
In the standard deviation equation:
- The lowercase Greek sigma, σ, represents the standard deviation
- N is the number of items in the set
- The uppercase Greek sigma, ∑, means to add up the values to its right (in this case, the sums of the squares of the differences between the xi values and μ) as i ranges from 1 to N
- The lowercase Greek mu, μ, is the mean (average) of the values
Write a program similar to the one shown in the following screenshot to test your extension methods. This program generates the indicated number of values and displays statistics about them. Each value is the sum of two random values between 1 and 6, so the values give a bell curve. (The shape is more obvious if you generate more than 100 values.):
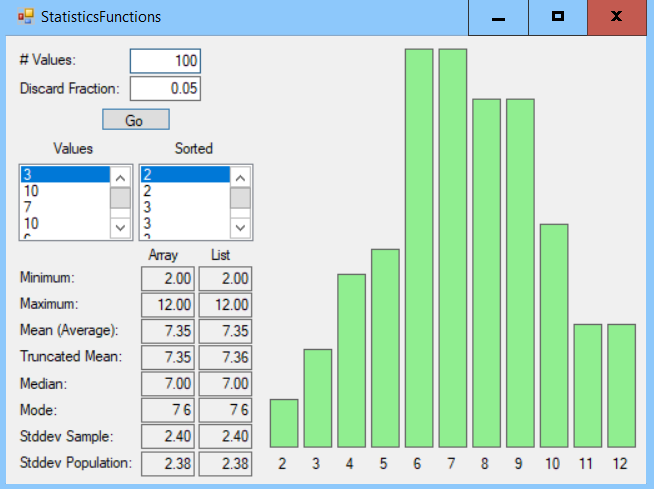
The example solution uses labels to build the histogram, showing the numbers' frequencies.
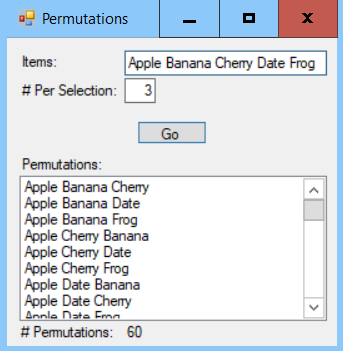
A permutation is an ordering of a selection of objects from a set. For example, suppose the set is {apple, banana, cherry}, then the permutations containing two items are all of the orderings of two items selected from that set. Those permutations are {apple, banana}, {apple, cherry}, {banana, apple}, {banana, cherry}, {cherry, apple}, and {cherry, banana}. Notice that {apple, banana} and {banana, apple} contain the same items in different orders.
Write an extension method that returns a List<List<T>>, holding the permutations of a specified length from an array of items. If the specified length is omitted, return all permutations of all lengths.
Write a program similar to the one shown in the following screenshot to test your method:
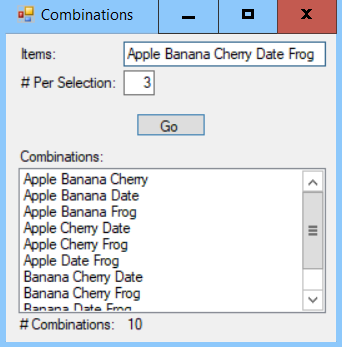
A combination is an unordered selection of objects from a set. For example, if the set is {apple, banana, cherry}, then the combinations containing two items are all of the subsets containing two items in any order. Those combinations are {apple, banana}, {apple, cherry}, and {banana, cherry}. This time, {apple, banana} and {banana, apple} are considered the same, so the combinations only include one of those subsets.
Write an extension method that returns a List<List<T>>, holding the combinations of a specified length from an array of items. If the specified length is zero, return all combinations of all lengths.
Write a program similar to the one shown in the following screenshot to test your method:
The factorial of a non-negative integer number, N, is written N! and is given by the equation N! = 1 × 2 × 3 × ... × N. You can also define factorials recursively as N! = N × (N – 1)! By definition, 0! = 1.
Write a program that calculates factorials recursively and non-recursively. Is one version better than the other? What is the limiting factor for calculating factorials?
The following equations define Fibonacci numbers recursively:
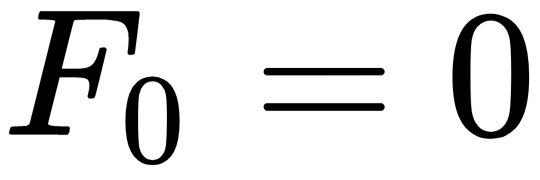
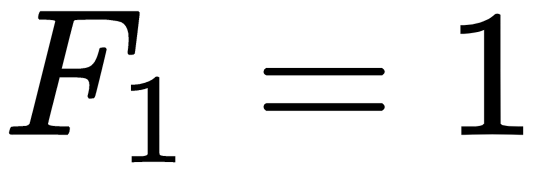
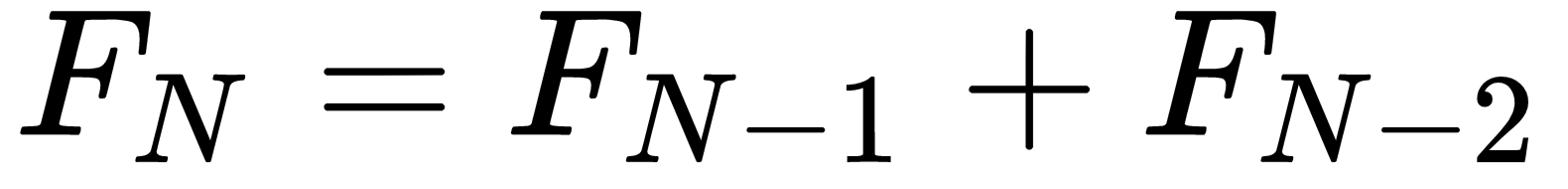
The last equation applies when N > 1. For example, the first ten Fibonacci numbers are 0, 1, 1, 2, 3, 5, 8, 13, 21, and 34.
Write a program that calculates Fibonacci numbers recursively, non-recursively, and via a cache table holding Fibonacci values.
The binomial coefficient of N and K gives the number of ways that you can pick N values from a set of K values. The binomial coefficient is usually written as
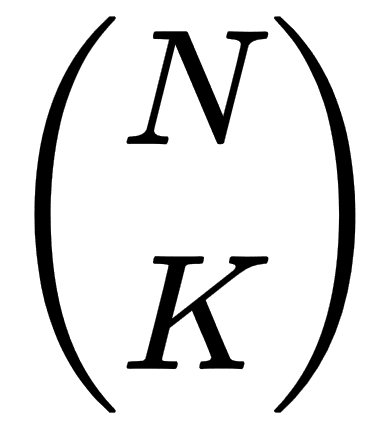
and is pronounced N choose K.
For example, suppose you have a set of four values, {A, B, C, D}. The possible ways to select two of those values are {A, B}, {A, C}, {A, D}, {B, C}, {B, D}, and {C, D}. There are six possible ways to select two items from the original set of four items, so
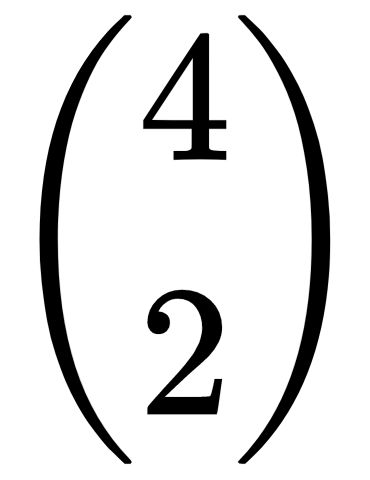
=6.
You can use the following formula to calculate binomial coefficients:
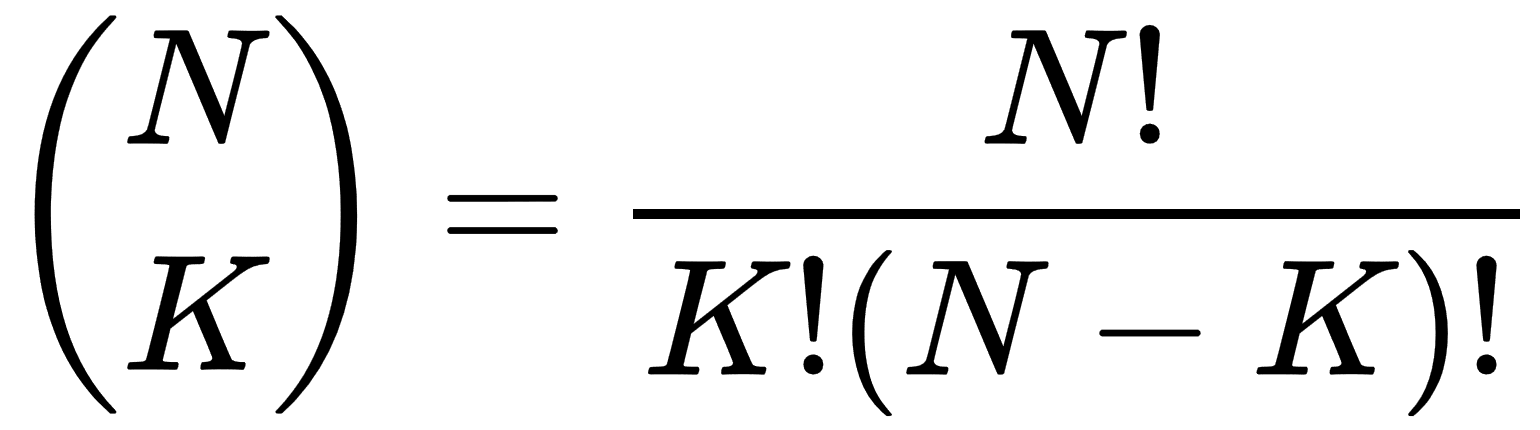
For the example where we select two items out of four, the formula gives the following:
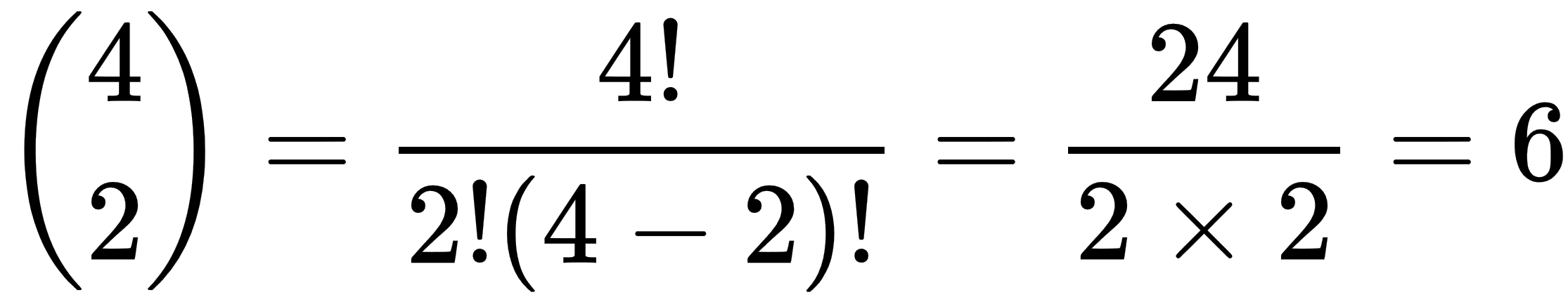
Write a program that calculates binomial coefficients. Test your program by verifying the following values:
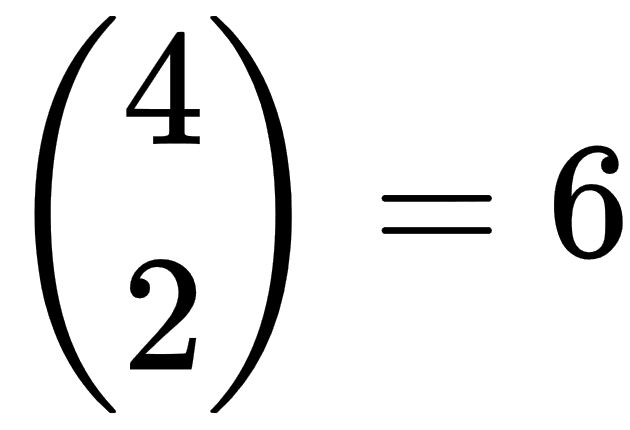
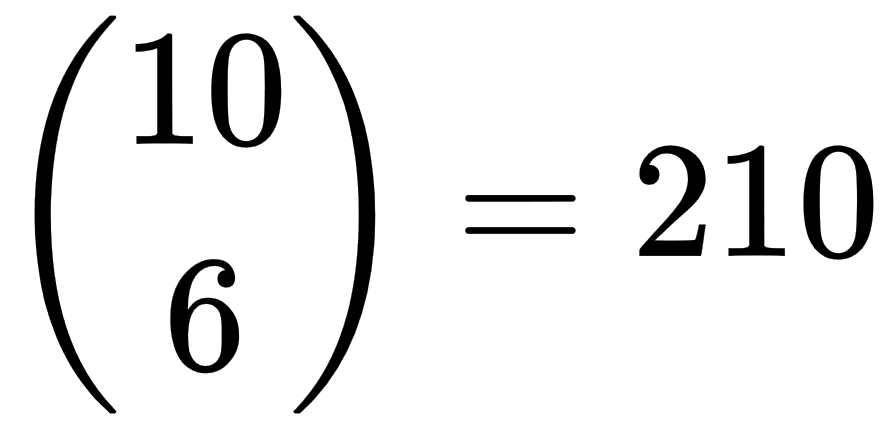
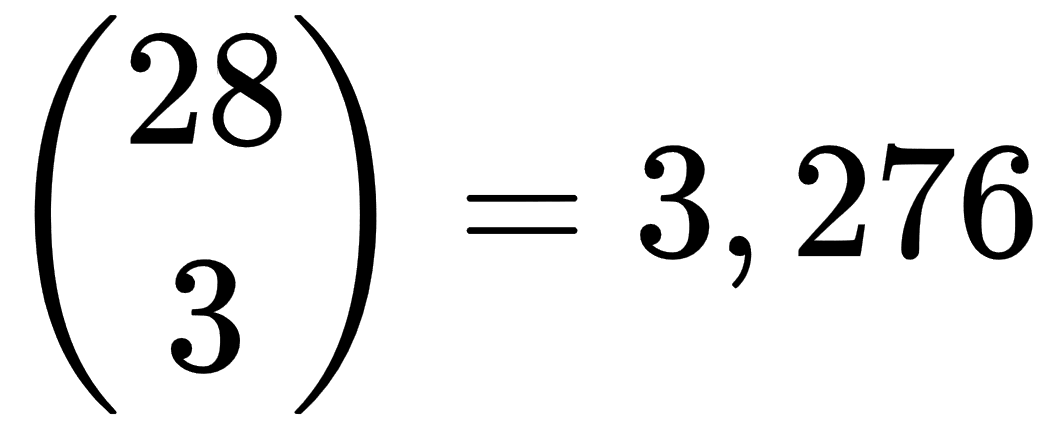
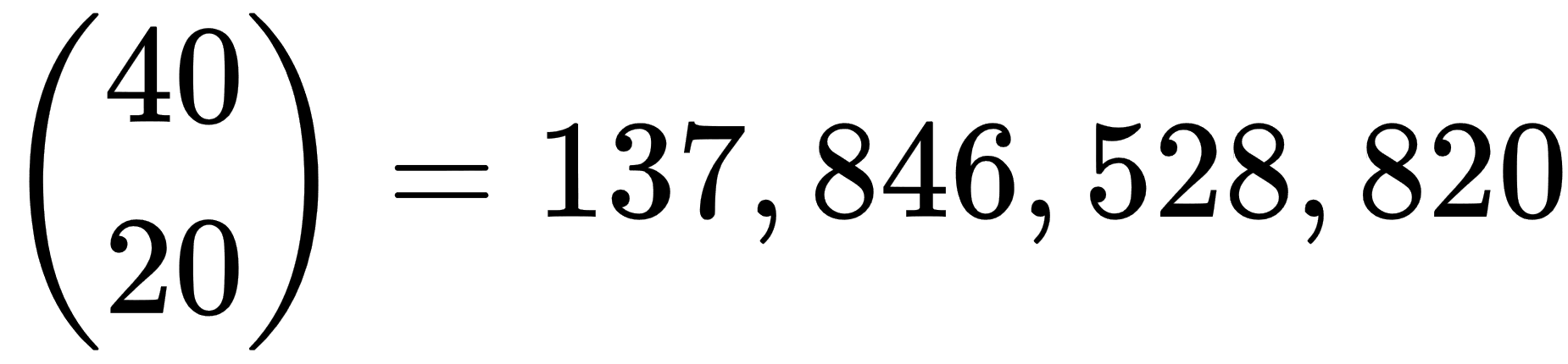
Pascal's triangle is a triangle of numbers (you probably guessed that from its name) where each row begins and ends with 1 and every other value is the sum of the two numbers above it. The following diagram shows the first six rows of Pascal's triangle:

Write a program that displays Pascal's triangle as simple text. For a bigger challenge, display the values graphically centered over each other, as shown in the preceding figure.
The greatest common divisor or GCD of two integers A and B, which is written GCD(A, B), is the largest integer C that divides both A and B evenly. For example, GCD(84, 36) = 12 because 12 is the largest integer that divides into both 84 and 36 with no remainder.
Write a program that calculates GCDs. Use the program to verify that GCD(10370370276, 82962962964) = 756.
The least common multiple or LCM of two positive integers A and B, which is written LCM(A, B), is the smallest positive integer that is a multiple of both A and B. For example, LCM(30, 42) is 210 because 210 is the smallest positive integer that is a multiple of 30 (210 = 7 × 30) and 42 (210 = 5 × 42).
Write a program that calculates LCMs. Use the program to verify that LCM(1234567000, 7654321000) = 9,449,772,114,007,000.
Write a program that calculates the sums of multiples of 3 or 5 between zero and a given maximum value. For example, if the maximum is 30, then the program should calculate 3 + 5 + 6 + 9 + 10 + 12 + 15 + 18 + 20 + 21 + 24 + 25 + 27 + 30 = 225 because those are the multiples of 3 and 5.
A prime number is an integer greater than 1 that has no factors other than 1 and itself. For example, 17 is prime because the only positive integers that you can multiply to get 17 are 1 and 17. In contrast, 21 is not prime because 3 × 7 = 21. Integers greater than 1 that are not prime are called composite numbers.
Write a program that determines whether an integer is prime or composite.
Write a program that builds an array of Booleans that indicates which values up to a specified maximum are prime. For example, if you call the array Primes, then Primes[i] should be true if i is prime. After it builds the table, the program should use it to display the largest prime that it found.
A number's prime factors are a set of prime numbers that multiply together to give the original number. For example, 60 = 2 × 2 × 3 × 5. There is only one set of prime numbers that can multiply together to give a particular number, so the prime factorization is unique.
Write a program that prime factors numbers.
A number's unique prime factors are the set of the number's prime factors with duplicates removed. For example, the prime factors of 360 are {2, 2, 2, 3, 3, 5}. Its unique prime factors are {2, 3, 5}.
Write a program that finds a number's unique prime factors.
Mathematicians like playing with prime numbers, so they have come up with several different names for groupings of related primes:
- Twin primes are primes {p, p + 2} that differ by two, such as {3, 5}. (Primes that differ by only 1 are not very interesting because 2 and 3 are the only primes that differ by 1.)
- Cousin primes are primes {p, p + 4} that differ by 4, such as {3, 7}.
- Sexy primes are primes {p, p + 6} that differ by 6, such as {5, 11}. (The name sexy primes is a pun because sex is Latin for six.)
You can also look for different numbers of primes with various spacings. For example, you can look for sexy pairs, sexy triples such as {7, 13, 19}, and so forth.
Write a program that checks numbers up to a maximum value, looking for primes with a given spacing and quantity. For example, the user might set the spacing to six and the number to 3 to look for groups of three primes that are each six apart, such as {5, 11, 17}.
Use your program to see what's special about groups of three or four primes that differ by 6, 12, 18, and other multiples of 3.
A divisor of a number N is any number that divides evenly into N. For example, the divisors of 12 are {1, 2, 4, 6, 12}.
The proper divisors of a number N are N's divisors, not including N itself. For example, the proper divisors of 12 are {1, 2, 4, 6}.
Write a program that finds a number's proper divisors.
Two numbers are amicable numbers if they are different and the sum of each number's proper divisors equals the other number. For example, the divisors of 220 are {1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110} and 1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284. Also, the divisors of 284 are {1, 2, 4, 71, 142} and 1 + 2 + 4 + 71 + 142 = 220. That means 220 and 284 are amicable numbers.
Write a program that finds amicable numbers between 1 and a specified maximum.
A perfect number equals the sum of its divisors. Basically, a perfect number is amicable with itself. For example, the divisors of 6 are 1, 2, and 3, and 6 = 1 + 2 + 3.
Write a program that finds perfect numbers between 1 and a specified maximum.
A number is an Armstrong number if raising its digits to the power of the number of digits and adding the results give the original number. For example, 371 is an Armstrong number because it has three digits and 33 + 73 + 13 = 371.
Write a program that finds Armstrong numbers between 1 and a specified maximum.





