Book Image

Python: End-to-end Data Analysis

By : Ivan Idris, Luiz Felipe Martins, Martin Czygan, Phuong Vo.T.H, Magnus Vilhelm Persson
Book Image

Python: End-to-end Data Analysis

By: Ivan Idris, Luiz Felipe Martins, Martin Czygan, Phuong Vo.T.H, Magnus Vilhelm Persson

Overview of this book

Data analysis is the process of applying logical and analytical reasoning to study each component of data present in the system. Python is a multi-domain, high-level, programming language that offers a range of tools and libraries suitable for all purposes, it has slowly evolved as one of the primary languages for data science. Have you ever imagined becoming an expert at effectively approaching data analysis problems, solving them, and extracting all of the available information from your data? If yes, look no further, this is the course you need! In this course, we will get you started with Python data analysis by introducing the basics of data analysis and supported Python libraries such as matplotlib, NumPy, and pandas. Create visualizations by choosing color maps, different shapes, sizes, and palettes then delve into statistical data analysis using distribution algorithms and correlations. You’ll then find your way around different data and numerical problems, get to grips with Spark and HDFS, and set up migration scripts for web mining. You’ll be able to quickly and accurately perform hands-on sorting, reduction, and subsequent analysis, and fully appreciate how data analysis methods can support business decision-making. Finally, you will delve into advanced techniques such as performing regression, quantifying cause and effect using Bayesian methods, and discovering how to use Python’s tools for supervised machine learning. The course provides you with highly practical content explaining data analysis with Python, from the following Packt books: 1. Getting Started with Python Data Analysis. 2. Python Data Analysis Cookbook. 3. Mastering Python Data Analysis. By the end of this course, you will have all the knowledge you need to analyze your data with varying complexity levels, and turn it into actionable insights.

Related Content you might be interested in

Current Title:

Small book image
Python: End-to-end Data Analysis
Ivan Idris | Luiz Felipe Martins | Martin Czygan | Phuong Vo.T.H | Magnus Vilhelm Persson
May, 2017 | 15 hours 31 minutes
No titles found
Table of Contents (6 chapters)
Preface
Preface
What this learning path covers
What you need for this learning path
Who this learning path is for
Reader feedback
Customer support
Downloading the example code
Errata
Piracy
Free Chapter
1
1. Module 1
1. Module 1
1. Introducing Data Analysis and Libraries
2. NumPy Arrays and Vectorized Computation
3. Data Analysis with Pandas
4. Data Visualization
5. Time Series
6. Interacting with Databases
7. Data Analysis Application Examples
8. Machine Learning Models with scikit-learn
2
2. Module 2
2. Module 2
1. Laying the Foundation for Reproducible Data Analysis
2. Creating Attractive Data Visualizations
3. Statistical Data Analysis and Probability
4. Dealing with Data and Numerical Issues
5. Web Mining, Databases, and Big Data
6. Signal Processing and Timeseries
7. Selecting Stocks with Financial Data Analysis
8. Text Mining and Social Network Analysis
9. Ensemble Learning and Dimensionality Reduction
10. Evaluating Classifiers, Regressors, and Clusters
11. Analyzing Images
12. Parallelism and Performance
A. Glossary
B. Function Reference
C. Online Resources
D. Tips and Tricks for Command-Line and Miscellaneous Tools
3
3. Module 3
3. Module 3
1. Tools of the Trade
2. Exploring Data
3. Learning About Models
4. Regression
5. Clustering
6. Bayesian Methods
7. Supervised and Unsupervised Learning
8. Time Series Analysis
E. More on Jupyter Notebook and matplotlib Styles
4
A. Bibliography
A. Bibliography
5
Index
Index

NumPy is the fundamental package supported for presenting and computing data with high performance in Python. It provides some interesting features as follows:

NumPy is a good starting package for you to get familiar with arrays and array-oriented computing in data analysis. Also, it is the basic step to learn other, more effective tools such as Pandas, which we will see in the next chapter. We will be using NumPy version 1.9.1.

An array can be used to contain values of a data object in an experiment or simulation step, pixels of an image, or a signal recorded by a measurement device. For example, the latitude of the Eiffel Tower, Paris is 48.858598 and the longitude is 2.294495. It can be presented in a NumPy array object as p:

>>> import numpy as np
>>> p = np.array([48.858598, 2.294495])
>>> p
array([48.858598, 2.294495])

This is a manual construction of an array using the np.array function. The standard convention to import NumPy is as follows:

>>> import numpy as np

You can, of course, put from numpy import * in your code to avoid having to write np. However, you should be careful with this habit because of the potential code conflicts (further information on code conventions can be found in the Python Style Guide, also known as PEP8, at https://www.python.org/dev/peps/pep-0008/).

There are two requirements of a NumPy array: a fixed size at creation and a uniform, fixed data type, with a fixed size in memory. The following functions help you to get information on the p matrix:

>>> p.ndim    # getting dimension of array p
1
>>> p.shape   # getting size of each array dimension
(2,)
>>> len(p)    # getting dimension length of array p
2
>>> p.dtype    # getting data type of array p
dtype('float64')

There are five basic numerical types including Booleans (bool), integers (int), unsigned integers (uint), floating point (float), and complex. They indicate how many bits are needed to represent elements of an array in memory. Besides that, NumPy also has some types, such as intc and intp, that have different bit sizes depending on the platform.

See the following table for a listing of NumPy's supported data types:

Type

Type code

Description

Range of value

bool

 

Boolean stored as a byte

True/False

intc

 

Similar to C int (int32 or int 64)

 

intp

 

Integer used for indexing (same as C size_t)

 

int8, uint8

i1, u1

Signed and unsigned 8-bit integer types

int8: (-128 to 127)

uint8: (0 to 255)

int16, uint16

i2, u2

Signed and unsigned 16-bit integer types

int16: (-32768 to 32767)

uint16: (0 to 65535)

int32, uint32

I4, u4

Signed and unsigned 32-bit integer types

int32: (-2147483648 to 2147483647

uint32: (0 to 4294967295)

int64, uinit64

i8, u8

Signed and unsigned 64-bit integer types

Int64: (-9223372036854775808 to 9223372036854775807)

uint64: (0 to 18446744073709551615)

float16

f2

Half precision float: sign bit, 5 bits exponent, and 10b bits mantissa

 

float32

f4 / f

Single precision float: sign bit, 8 bits exponent, and 23 bits mantissa

 

float64

f8 / d

Double precision float: sign bit, 11 bits exponent, and 52 bits mantissa

 

complex64, complex128, complex256

c8, c16, c32

Complex numbers represented by two 32-bit, 64-bit, and 128-bit floats

 

object

0

Python object type

 

string_

S

Fixed-length string type

Declare a string dtype with length 10, using S10

unicode_

U

Fixed-length Unicode type

Similar to string_ example, we have 'U10'

We can easily convert or cast an array from one dtype to another using the astype method:

>>> a = np.array([1, 2, 3, 4])
>>> a.dtype
dtype('int64')
>>> float_b = a.astype(np.float64)
>>> float_b.dtype
dtype('float64')

Note

The astype function will create a new array with a copy of data from an old array, even though the new dtype is similar to the old one.

There are various functions provided to create an array object. They are very useful for us to create and store data in a multidimensional array in different situations.

Now, in the following table we will summarize some of NumPy's common functions and their use by examples for array creation:

Function

Description

Example

empty, empty_like

Create a new array of the given shape and type, without initializing elements

>>> np.empty([3,2], dtype=np.float64)
array([[0., 0.], [0., 0.], [0., 0.]])
>>> a = np.array([[1, 2], [4, 3]])
>>> np.empty_like(a)
array([[0, 0], [0, 0]])

eye, identity

Create a NxN identity matrix with ones on the diagonal and zero elsewhere

>>> np.eye(2, dtype=np.int)
array([[1, 0], [0, 1]])

ones, ones_like

Create a new array with the given shape and type, filled with 1s for all elements

>>> np.ones(5)
array([1., 1., 1., 1., 1.])
>>> np.ones(4, dtype=np.int)
array([1, 1, 1, 1])
>>> x = np.array([[0,1,2], [3,4,5]])
>>> np.ones_like(x)
array([[1, 1, 1],[1, 1, 1]])

zeros, zeros_like

This is similar to ones, ones_like, but initializing elements with 0s instead

>>> np.zeros(5)
array([0., 0., 0., 0-, 0.])
>>> np.zeros(4, dtype=np.int)
array([0, 0, 0, 0])
>>> x = np.array([[0, 1, 2], [3, 4, 5]])
>>> np.zeros_like(x)
array([[0, 0, 0],[0, 0, 0]])

arange

Create an array with even spaced values in a given interval

>>> np.arange(2, 5)
array([2, 3, 4])
>>> np.arange(4, 12, 5)
array([4, 9])

full, full_like

Create a new array with the given shape and type, filled with a selected value

>>> np.full((2,2), 3, dtype=np.int)
array([[3, 3], [3, 3]])
>>> x = np.ones(3)
>>> np.full_like(x, 2)
array([2., 2., 2.])

array

Create an array from the existing data

>>> np.array([[1.1, 2.2, 3.3], [4.4, 5.5, 6.6]])
array([1.1, 2.2, 3.3], [4.4, 5.5, 6.6]])

asarray

Convert the input to an array

>>> a = [3.14, 2.46]
>>> np.asarray(a)
array([3.14, 2.46])

copy

Return an array copy of the given object

>>> a = np.array([[1, 2], [3, 4]])
>>> np.copy(a)
array([[1, 2], [3, 4]])

fromstring

Create 1-D array from a string or text 

>>> np.fromstring('3.14 2.17', dtype=np.float, sep=' ')
array([3.14, 2.17])

As with other Python sequence types, such as lists, it is very easy to access and assign a value of each array's element:

>>> a = np.arange(7)
>>> a
array([0, 1, 2, 3, 4, 5, 6])
>>> a[1], a [4], a[-1]
(1, 4, 6)

Note

In Python, array indices start at 0. This is in contrast to Fortran or Matlab, where indices begin at 1.

As another example, if our array is multidimensional, we need tuples of integers to index an item:

>>> a = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
>>> a[0, 2]      # first row, third column
3
>>> a[0, 2] = 10
>>> a
array([[1, 2, 10], [4, 5, 6], [7, 8, 9]])
>>> b = a[2]
>>> b
array([7, 8, 9])
>>> c = a[:2]
>>> c
array([[1, 2, 10], [4, 5, 6]])

We call b and c as array slices, which are views on the original one. It means that the data is not copied to b or c, and whenever we modify their values, it will be reflected in the array a as well:

>>> b[-1] = 11
>>> a
array([[1, 2, 10], [4, 5, 6], [7, 8, 11]])

Note

We use a colon (:) character to take the entire axis when we omit the index number.

Besides indexing with slices, NumPy also supports indexing with Boolean or integer arrays (masks). This method is called fancy indexing. It creates copies, not views.

First, we take a look at an example of indexing with a Boolean mask array:

>>> a = np.array([3, 5, 1, 10])
>>> b = (a % 5 == 0)
>>> b
array([False, True, False, True], dtype=bool)
>>> c = np.array([[0, 1], [2, 3], [4, 5], [6, 7]])
>>> c[b]
array([[2, 3], [6, 7]])

The second example is an illustration of using integer masks on arrays:

>>> a = np.array([[1, 2, 3, 4], 
 [5, 6, 7, 8], 
 [9, 10, 11, 12],
 [13, 14, 15, 16]])
>>> a[[2, 1]]
array([[9, 10, 11, 12], [5, 6, 7, 8]])
>>> a[[-2, -1]]          # select rows from the end
array([[ 9, 10, 11, 12], [13, 14, 15, 16]])
>>> a[[2, 3], [0, 1]]    # take elements at (2, 0) and (3, 1)
array([9, 14])

Note

The mask array must have the same length as the axis that it's indexing.

Tip

Downloading the example code

You can download the example code files for all Packt books you have purchased from your account at http://www.packtpub.com. If you purchased this book elsewhere, you can visit http://www.packtpub.com/support and register to have the files e-mailed directly to you.

We are getting familiar with creating and accessing ndarrays. Now, we continue to the next step, applying some mathematical operations to array data without writing any for loops, of course, with higher performance.

Scalar operations will propagate the value to each element of the array:

>>> a = np.ones(4)
>>> a * 2
array([2., 2., 2., 2.])
>>> a + 3
array([4., 4., 4., 4.])

All arithmetic operations between arrays apply the operation element wise:

>>> a = np.ones([2, 4])
>>> a * a
array([[1., 1., 1., 1.], [1., 1., 1., 1.]])
>>> a + a
array([[2., 2., 2., 2.], [2., 2., 2., 2.]])

Also, here are some examples of comparisons and logical operations:

>>> a = np.array([1, 2, 3, 4])
>>> b = np.array([1, 1, 5, 3])
>>> a == b
array([True, False, False, False], dtype=bool)

>>> np.array_equal(a, b)      # array-wise comparison
False

>>> c = np.array([1, 0])
>>> d = np.array([1, 1])
>>> np.logical_and(c, d)      # logical operations
array([True, False])

Many helpful array functions are supported in NumPy for analyzing data. We will list some part of them that are common in use. Firstly, the transposing function is another kind of reshaping form that returns a view on the original data array without copying anything:

>>> a = np.array([[0, 5, 10], [20, 25, 30]])
>>> a.reshape(3, 2)
array([[0, 5], [10, 20], [25, 30]])
>>> a.T
array([[0, 20], [5, 25], [10, 30]])

In general, we have the swapaxes method that takes a pair of axis numbers and returns a view on the data, without making a copy:

>>> a = np.array([[[0, 1, 2], [3, 4, 5]], 
 [[6, 7, 8], [9, 10, 11]]])
>>> a.swapaxes(1, 2)
array([[[0, 3],
    [1, 4],
    [2, 5]],
   [[6, 9],
    [7, 10],
    [8, 11]]])

The transposing function is used to do matrix computations; for example, computing the inner matrix product XT.X using np.dot:

>>> a = np.array([[1, 2, 3],[4,5,6]])
>>> np.dot(a.T, a)
array([[17, 22, 27],
   [22, 29, 36],
   [27, 36, 45]])

Sorting data in an array is also an important demand in processing data. Let's take a look at some sorting functions and their use:

>>> a = np.array ([[6, 34, 1, 6], [0, 5, 2, -1]])

>>> np.sort(a)     # sort along the last axis
array([[1, 6, 6, 34], [-1, 0, 2, 5]])

>>> np.sort(a, axis=0)    # sort along the first axis
array([[0, 5, 1, -1], [6, 34, 2, 6]])

>>> b = np.argsort(a)    # fancy indexing of sorted array
>>> b
array([[2, 0, 3, 1], [3, 0, 2, 1]])
>>> a[0][b[0]]
array([1, 6, 6, 34])

>>> np.argmax(a)    # get index of maximum element
1

See the following table for a listing of array functions:

Function

Description

Example

sin, cos, tan, cosh, sinh, tanh, arcos, arctan, deg2rad

Trigonometric and hyperbolic functions

>>> a = np.array([0.,30., 45.])
>>> np.sin(a * np.pi / 180)
array([0., 0.5, 0.7071678])

around, round, rint, fix, floor, ceil, trunc

Rounding elements of an array to the given or nearest number

>>> a = np.array([0.34, 1.65])
>>> np.round(a)
array([0., 2.])

sqrt, square, exp, expm1, exp2, log, log10, log1p, logaddexp

Computing the exponents and logarithms of an array

>>> np.exp(np.array([2.25, 3.16]))
array([9.4877, 23.5705])

add, negative, multiply, devide, power, substract, mod, modf, remainder

Set of arithmetic functions on arrays

>>> a = np.arange(6)
>>> x1 = a.reshape(2,3)
>>> x2 = np.arange(3)
>>> np.multiply(x1, x2)
array([[0,1,4],[0,4,10]])

greater, greater_equal, less, less_equal, equal, not_equal

Perform elementwise comparison: >, >=, <, <=, ==, !=

>>> np.greater(x1, x2)
array([[False, False, False], [True, True, True]], dtype = bool)

With the NumPy package, we can easily solve many kinds of data processing tasks without writing complex loops. It is very helpful for us to control our code as well as the performance of the program. In this part, we want to introduce some mathematical and statistical functions.

See the following table for a listing of mathematical and statistical functions:

Function

Description

Example

sum

Calculate the sum of all the elements in an array or along the axis

>>> a = np.array([[2,4], [3,5]])
>>> np.sum(a, axis=0)
array([5, 9])

prod

Compute the product of array elements over the given axis

>>> np.prod(a, axis=1)
array([8, 15])

diff

Calculate the discrete difference along the given axis

>>> np.diff(a, axis=0)
array([[1,1]])

gradient

Return the gradient of an array

>>> np.gradient(a)
[array([[1., 1.], [1., 1.]]), array([[2., 2.], [2., 2.]])]

cross

Return the cross product of two arrays

>>> b = np.array([[1,2], [3,4]])
>>> np.cross(a,b)
array([0, -3])

std, var

Return standard deviation and variance of arrays 

>>> np.std(a)
1.1180339
>>> np.var(a)
1.25

mean

Calculate arithmetic mean of an array

>>> np.mean(a)
3.5

where

Return elements, either from x or y, that satisfy a condition

>>> np.where([[True, True], [False, True]], [[1,2],[3,4]], [[5,6],[7,8]])
array([[1,2], [7, 4]])

unique

Return the sorted unique values in an array

>>> id = np.array(['a', 'b', 'c', 'c', 'd'])
>>> np.unique(id)
array(['a', 'b', 'c', 'd'], dtype='|S1')

intersect1d

Compute the sorted and common elements in two arrays

>>> a = np.array(['a', 'b', 'a', 'c', 'd', 'c'])
>>> b = np.array(['a', 'xyz', 'klm', 'd'])
>>> np.intersect1d(a,b)
array(['a', 'd'], dtype='|S3')

We can also save and load data to and from a disk, either in text or binary format, by using different supported functions in NumPy package.

Arrays are saved by default in an uncompressed raw binary format, with the file extension .npy by the np.save function:

>>> a = np.array([[0, 1, 2], [3, 4, 5]])
>>> np.save('test1.npy', a)

Note

The library automatically assigns the .npy extension, if we omit it.

If we want to store several arrays into a single file in an uncompressed .npz format, we can use the np.savez function, as shown in the following example:

>>> a = np.arange(4)
>>> b = np.arange(7)
>>> np.savez('test2.npz', arr0=a, arr1=b)

The .npz file is a zipped archive of files named after the variables they contain. When we load an .npz file, we get back a dictionary-like object that can be queried for its lists of arrays:

>>> dic = np.load('test2.npz')
>>> dic['arr0']
array([0, 1, 2, 3])

Another way to save array data into a file is using the np.savetxt function that allows us to set format properties in the output file:

>>> x = np.arange(4)
>>> # e.g., set comma as separator between elements
>>> np.savetxt('test3.out', x, delimiter=',')

We have two common functions such as np.load and np.loadtxt, which correspond to the saving functions, for loading an array:

>>> np.load('test1.npy')
array([[0, 1, 2], [3, 4, 5]])
>>> np.loadtxt('test3.out', delimiter=',')
array([0., 1., 2., 3.])

Similar to the np.savetxt function, the np.loadtxt function also has a lot of options for loading an array from a text file.

Loading and saving data

We can also save and load data to and from a disk, either in text or binary format, by using different supported functions in NumPy package.

Arrays are saved by default in an uncompressed raw binary format, with the file extension .npy by the np.save function:

>>> a = np.array([[0, 1, 2], [3, 4, 5]])
>>> np.save('test1.npy', a)

Note

The library automatically assigns the .npy extension, if we omit it.

If we want to store several arrays into a single file in an uncompressed .npz format, we can use the np.savez function, as shown in the following example:

>>> a = np.arange(4)
>>> b = np.arange(7)
>>> np.savez('test2.npz', arr0=a, arr1=b)

The .npz file is a zipped archive of files named after the variables they contain. When we load an .npz file, we get back a dictionary-like object that can be queried for its lists of arrays:

>>> dic = np.load('test2.npz')
>>> dic['arr0']
array([0, 1, 2, 3])

Another way to save array data into a file is using the np.savetxt function that allows us to set format properties in the output file:

>>> x = np.arange(4)
>>> # e.g., set comma as separator between elements
>>> np.savetxt('test3.out', x, delimiter=',')

We have two common functions such as np.load and np.loadtxt, which correspond to the saving functions, for loading an array:

>>> np.load('test1.npy')
array([[0, 1, 2], [3, 4, 5]])
>>> np.loadtxt('test3.out', delimiter=',')
array([0., 1., 2., 3.])

Similar to the np.savetxt function, the np.loadtxt function also has a lot of options for loading an array from a text file.

Saving an array

Arrays are

saved by default in an uncompressed raw binary format, with the file extension .npy by the np.save function:

>>> a = np.array([[0, 1, 2], [3, 4, 5]])
>>> np.save('test1.npy', a)

Note

The library automatically assigns the .npy extension, if we omit it.

If we want to store several arrays into a single file in an uncompressed .npz format, we can use the np.savez function, as shown in the following example:

>>> a = np.arange(4)
>>> b = np.arange(7)
>>> np.savez('test2.npz', arr0=a, arr1=b)

The .npz file is a zipped archive of files named after the variables they contain. When we load an .npz file, we get back a dictionary-like object that can be queried for its lists of arrays:

>>> dic = np.load('test2.npz')
>>> dic['arr0']
array([0, 1, 2, 3])

Another way to save array data into a file is using the np.savetxt function that allows us to set format properties in the output file:

>>> x = np.arange(4)
>>> # e.g., set comma as separator between elements
>>> np.savetxt('test3.out', x, delimiter=',')

We have two common functions such as np.load and np.loadtxt, which correspond to the saving functions, for loading an array:

>>> np.load('test1.npy')
array([[0, 1, 2], [3, 4, 5]])
>>> np.loadtxt('test3.out', delimiter=',')
array([0., 1., 2., 3.])

Similar to the np.savetxt function, the np.loadtxt function also has a lot of options for loading an array from a text file.

Loading an array

We have two

common functions such as np.load and np.loadtxt, which correspond to the saving functions, for loading an array:

>>> np.load('test1.npy')
array([[0, 1, 2], [3, 4, 5]])
>>> np.loadtxt('test3.out', delimiter=',')
array([0., 1., 2., 3.])

Similar to the np.savetxt function, the np.loadtxt function also has a lot of options for loading an array from a text file.

Linear algebra is a branch of mathematics concerned with vector spaces and the mappings between those spaces. NumPy has a package called linalg that supports powerful linear algebra functions. We can use these functions to find eigenvalues and eigenvectors or to perform singular value decomposition:

>>> A = np.array([[1, 4, 6],
    [5, 2, 2],
    [-1, 6, 8]])
>>> w, v = np.linalg.eig(A)
>>> w                           # eigenvalues
array([-0.111 + 1.5756j, -0.111 – 1.5756j, 11.222+0.j])
>>> v                           # eigenvector
array([[-0.0981 + 0.2726j, -0.0981 – 0.2726j, 0.5764+0.j],
    [0.7683+0.j, 0.7683-0.j, 0.4591+0.j],
    [-0.5656 – 0.0762j, -0.5656 + 0.00763j, 0.6759+0.j]])

The function is implemented using the geev Lapack routines that compute the eigenvalues and eigenvectors of general square matrices.

Another common problem is solving linear systems such as Ax = b with A as a matrix and x and b as vectors. The problem can be solved easily using the numpy.linalg.solve function:

>>> A = np.array([[1, 4, 6], [5, 2, 2], [-1, 6, 8]])
>>> b = np.array([[1], [2], [3]])
>>> x = np.linalg.solve(A, b)
>>> x
array([[-1.77635e-16], [2.5], [-1.5]])

The following table will summarise some commonly used functions in the numpy.linalg package:

Function

Description

Example

dot

Calculate the dot product of two arrays

>>> a = np.array([[1, 0],[0, 1]])
>>> b = np.array( [[4, 1],[2, 2]])
>>> np.dot(a,b)
array([[4, 1],[2, 2]])

inner, outer

Calculate the inner and outer product of two arrays

>>> a = np.array([1, 1, 1])
>>> b = np.array([3, 5, 1])
>>> np.inner(a,b)
9

linalg.norm

Find a matrix or vector norm

>>> a = np.arange(3)
>>> np.linalg.norm(a)
2.23606

linalg.det

Compute the determinant of an array

>>> a = np.array([[1,2],[3,4]])
>>> np.linalg.det(a)
-2.0

linalg.inv

Compute the inverse of a matrix

>>> a = np.array([[1,2],[3,4]])
>>> np.linalg.inv(a)
array([[-2., 1.],[1.5, -0.5]])

linalg.qr

Calculate the QR decomposition

>>> a = np.array([[1,2],[3,4]])
>>> np.linalg.qr(a)
(array([[0.316, 0.948], [0.948, 0.316]]), array([[ 3.162, 4.427], [ 0., 0.632]]))

linalg.cond

Compute the condition number of a matrix

>>> a = np.array([[1,3],[2,4]])
>>> np.linalg.cond(a)
14.933034

trace

Compute the sum of the diagonal element

>>> np.trace(np.arange(6)).
reshape(2,3))
4

An important part of any simulation is the ability to generate random numbers. For this purpose, NumPy provides various routines in the submodule random. It uses a particular algorithm, called the Mersenne Twister, to generate pseudorandom numbers.

First, we need to define a seed that makes the random numbers predictable. When the value is reset, the same numbers will appear every time. If we do not assign the seed, NumPy automatically selects a random seed value based on the system's random number generator device or on the clock:

>>> np.random.seed(20)

An array of random numbers in the [0.0, 1.0] interval can be generated as follows:

>>> np.random.rand(5)
array([0.5881308, 0.89771373, 0.89153073, 0.81583748, 
         0.03588959])
>>> np.random.rand(5)
array([0.69175758, 0.37868094, 0.51851095, 0.65795147,  
       0.19385022])

>>> np.random.seed(20)    # reset seed number
>>> np.random.rand(5)
array([0.5881308, 0.89771373, 0.89153073, 0.81583748,  
       0.03588959])

If we want to generate random integers in the half-open interval [min, max], we can user the randint(min, max, length) function:

>>> np.random.randint(10, 20, 5)
array([17, 12, 10, 16, 18])

NumPy also provides for many other distributions, including the Beta, bionomial, chi-square, Dirichlet, exponential, F, Gamma, geometric, or Gumbel.

The following table will list some distribution functions and give examples for generating random numbers:

Function

Description

Example

binomial

Draw samples from a binomial distribution (n: number of trials, p: probability)

>>> n, p = 100, 0.2
>>> np.random.binomial(n, p, 3)
array([17, 14, 23])

dirichlet

Draw samples using a Dirichlet distribution

>>> np.random.dirichlet(alpha=(2,3), size=3)
array([[0.519, 0.480], [0.639, 0.36],
 [0.838, 0.161]])

poisson

Draw samples from a Poisson distribution

>>> np.random.poisson(lam=2, size= 2)
array([4,1])

normal

Draw samples using a normal Gaussian distribution

>>> np.random.normal
(loc=2.5, scale=0.3, size=3)
array([2.4436, 2.849, 2.741)

uniform

Draw samples using a uniform distribution

>>> np.random.uniform(
low=0.5, high=2.5, size=3)
array([1.38, 1.04, 2.19[)

We can also use the random number generation to shuffle items in a list. Sometimes this is useful when we want to sort a list in a random order:

>>> a = np.arange(10)
>>> np.random.shuffle(a)
>>> a
array([7, 6, 3, 1, 4, 2, 5, 0, 9, 8])

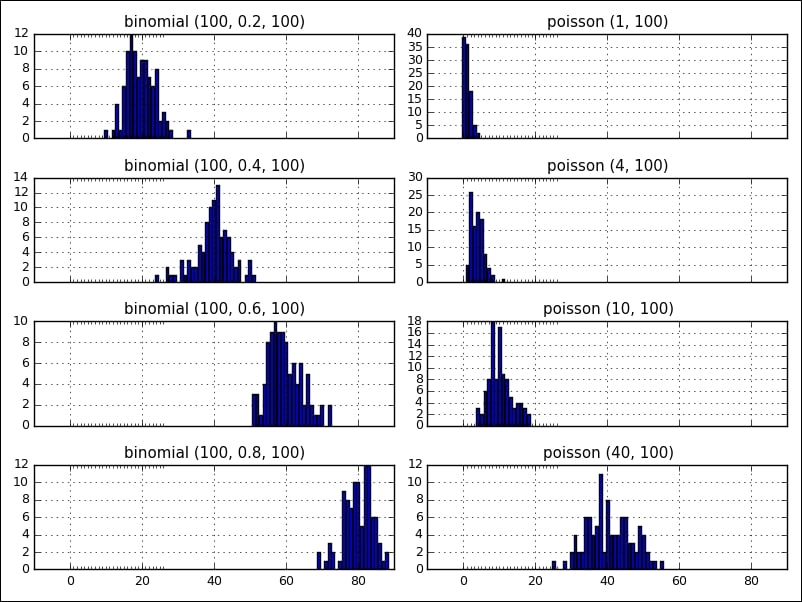
The following figure shows two distributions, binomial and poisson , side by side with various parameters (the visualization was created with matplotlib, which will be covered in Chapter 4, Data Visualization):

NumPy random numbers

In this chapter, we covered a lot of information related to the NumPy package, especially commonly used functions that are very helpful to process and analyze data in ndarray. Firstly, we learned the properties and data type of ndarray in the NumPy package. Secondly, we focused on how to create and manipulate an ndarray in different ways, such as conversion from other structures, reading an array from disk, or just generating a new array with given values. Thirdly, we studied how to access and control the value of each element in ndarray by using indexing and slicing.

Then, we are getting familiar with some common functions and operations on ndarray.

And finally, we continue with some advance functions that are related to statistic, linear algebra and sampling data. Those functions play important role in data analysis.

However, while NumPy by itself does not provide very much high-level data analytical functionality, having an understanding of it will help you use tools such as Pandas much more effectively. This tool will be discussed in the next chapter.

Practice exercises

Exercise 1: Using an array creation function, let's try to create arrays variable in the following situations:

Exercise 2: What is the difference between np.dot(a, b) and (a*b)?

Exercise 3: Consider the vector [1, 2, 3, 4, 5] building a new vector with four consecutive zeros interleaved between each value.

Exercise 4: Taking the data example file chapter2-data.txt, which includes information on a system log, solves the following tasks:

Previous Section
End of Section 3
Next Section