The QR decomposition, also known as the QR factorization, is another method of solving linear systems of equations using matrices, very much like the LU decomposition. The equation to solve is in the form of Ax=B, where matrix A=QR. However, in this case, A is a product of an orthogonal matrix, Q, and upper triangular matrix, R. The QR algorithm is commonly used to solve the linear least-squares problem.
An orthogonal matrix exhibits the following properties:
- It is a square matrix.
- Multiplying an orthogonal matrix by its transpose returns the identity matrix:
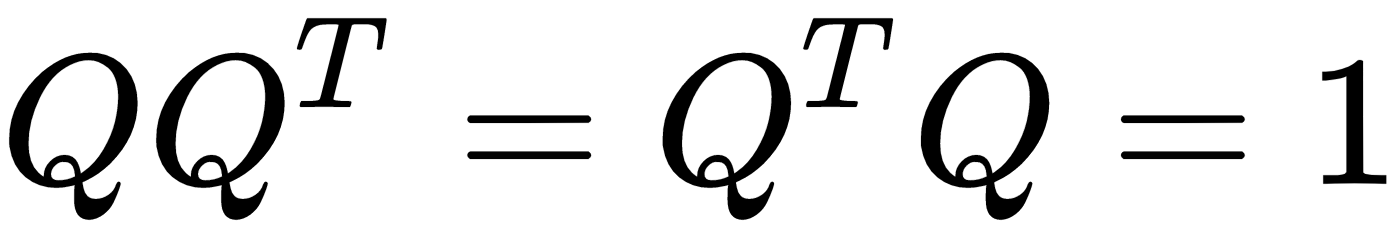
- The inverse of an orthogonal matrix equals its transpose:
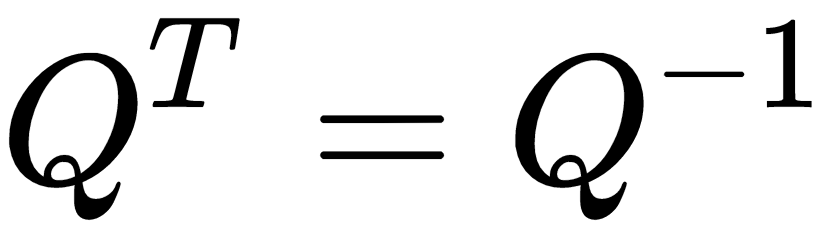
An identity matrix is also a square matrix, with its main diagonal containing 1s and 0s elsewhere.
The problem of Ax=B can now be restated as follows:
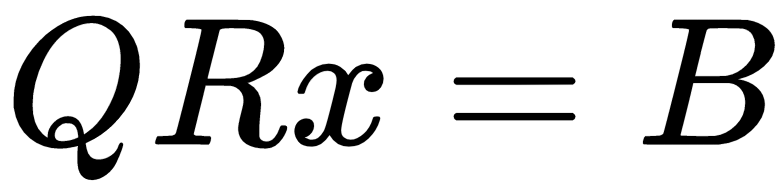

Using the same variables in the LU decomposition example, we will use the qr() method...



