Overview of this book
Transform IoT devices into intelligent systems with this comprehensive guide by Amita Kapoor, Chief AI Officer at Tipz AI. Drawing on 25 years of expertise in developing intelligent systems across industries, she demonstrates how to harness the combined power of artificial intelligence and IoT technology. A pioneer in making AI and neuroscience education accessible worldwide, Amita guides you through creating smart, efficient systems that leverage the latest advances in both fields. This new edition is updated with various optimization techniques in IoT used for enhancing efficiency and performance. It introduces you to cloud platforms such as Platform as a Service (PaaS) and Infrastructure as a Service (IaaS) for analyzing data generated using IoT devices. You’ll learn about machine learning algorithms, deep learning techniques, and practical applications in real-world IoT scenarios and advance to creating AI models that work with diverse data types, including time series, images, and audio. You’ll also harness the power of widely used Python libraries, TensorFlow and Keras, to build a variety of smart AI models.
*Email sign-up and proof of purchase required



 Free Chapter
Free Chapter

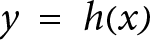 . This condition indicates that there is no slope at the minimum point, implying a “flat” spot or a turning point on the curve of
. This condition indicates that there is no slope at the minimum point, implying a “flat” spot or a turning point on the curve of 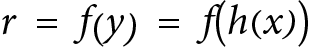 ) is positively definite. This condition ensures that the point is indeed a minimum, as a positive definite Hessian indicates that the function curves upwards
) is positively definite. This condition ensures that the point is indeed a minimum, as a positive definite Hessian indicates that the function curves upwards