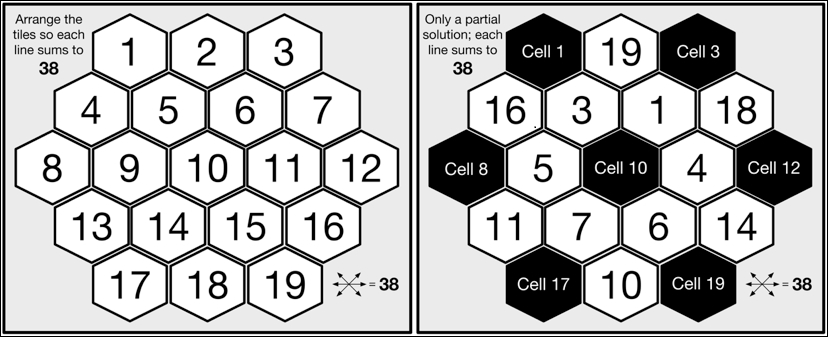
The puzzle we will solve is known as Aristotle's Number Puzzle, and this is a magic hexagon. The puzzle requires us to place 19 tiles, numbered 1 to 19, on a hexagonal grid such that each horizontal row and each diagonal across the board adds up to 38 when summing each of the numbers on each of the tiles in the corresponding line. The following, on the left-hand side, is a pictorial representation of the unsolved puzzle showing the hexagonal grid layout of the board with the tiles placed in order from the upper-left to the lower-right. Next to this, a partial solution to the puzzle is shown, where the two rows (starting with the tiles 16 and 11) and the four diagonals all add up to 38, with empty board cells in the positions 1, 3, 8, 10, 12, 17, and 19 and seven remaining unplaced tiles, 2, 8, 9, 12, 13, 15, and 17:
The mathematically minded among you will already have noticed that the number of possible tile layouts is the factorial 19; that is, there is a total of 121,645,100,408,832,000 unique combinations (ignoring rotational and mirror symmetry). Even when utilizing a modern microprocessor, it will clearly take a considerable period of time to find which of these 121 quadrillion combinations constitute a valid solution.
The algorithm we will use to solve the puzzle is a depth-first iterative search, allowing us to trade off limited memory for compute cycles; we could not feasibly store every possible board configuration without incurring huge expense.
Let's start our implementation by considering how to represent the board. The simplest way is to use a one-dimensional R vector of length 19, where the index i of the vector represents the corresponding ith cell on the board. Where a tile is not yet placed, the value of the board vector's "cell" will be the numeric 0.
empty_board <- c(0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0) partial_board <- c(0,19,0,16,3,1,18,0,5,0,4,0,11,7,6,14,0,10,0)
Next, let's define a function to evaluate whether the layout of tiles on the board represents a valid solution. As part of this, we need to specify the various combinations of board cells or "lines" that must add up to the target value 38, as follows:
all_lines <- list(
c(1,2,3), c(1,4,8), c(1,5,10,15,19),
c(2,5,9,13), c(2,6,11,16), c(3,7,12),
c(3,6,10,14,17), c(4,5,6,7), c(4,9,14,18),
c(7,11,15,18), c(8,9,10,11,12), c(8,13,17),
c(12,16,19), c(13,14,15,16), c(17,18,19)
)
evaluateBoard <- function(board)
{
for (line in all_lines) {
total <- 0
for (cell in line) {
total <- total + board[cell]
}
if (total != 38) return(FALSE)
}
return(TRUE) # We have a winner!
}In order to implement the depth-first solver, we need to manage the list of remaining tiles for the next tile placement. For this, we will utilize a variation on a simple stack by providing push and pop functions for both the first and last item within a vector. To make this distinct, we will implement it as a class and call it sequence.
Here is a simple S3-style class sequence that implements a double-ended head/tail stack by internally maintaining the stack's state within a vector:
sequence <- function()
{
sequence <- new.env() # Shared state for class instance
sequence$.vec <- vector() # Internal state of the stack
sequence$getVector <- function() return (.vec)
sequence$pushHead <- function(val) .vec <<- c(val, .vec)
sequence$pushTail <- function(val) .vec <<- c(.vec, val)
sequence$popHead <- function() {
val <- .vec[1]
.vec <<- .vec[-1] # Update must apply to shared state
return(val)
}
sequence$popTail <- function() {
val <- .vec[length(.vec)]
.vec <<- .vec[-length(.vec)]
return(val)
}
sequence$size <- function() return( length(.vec) )
# Each sequence method needs to use the shared state of the
# class instance, rather than its own function environment
environment(sequence$size) <- as.environment(sequence)
environment(sequence$popHead) <- as.environment(sequence)
environment(sequence$popTail) <- as.environment(sequence)
environment(sequence$pushHead) <- as.environment(sequence)
environment(sequence$pushTail) <- as.environment(sequence)
environment(sequence$getVector) <- as.environment(sequence)
class(sequence) <- "sequence"
return(sequence)
}The implementation of the sequence should be easy to understand from some example usage, as in the following:
> s <- sequence() ## Create an instance s of sequence > s$pushHead(c(1:5)) ## Initialize s with numbers 1 to 5 > s$getVector() [1] 1 2 3 4 5 > s$popHead() ## Take the first element from s [1] 1 > s$getVector() ## The number 1 has been removed from s [1] 2 3 4 5 > s$pushTail(1) ## Add number 1 as the last element in s > s$getVector() [1] 2 3 4 5 1
We are almost there. Here is the implementation of the placeTiles() function to perform the depth-first search:
01 placeTiles <- function(cells,board,tilesRemaining)
02 {
03 for (cell in cells) {
04 if (board[cell] != 0) next # Skip cell if not empty
05 maxTries <- tilesRemaining$size()
06 for (t in 1:maxTries) {
07 board[cell] = tilesRemaining$popHead()
08 retval <- placeTiles(cells,board,tilesRemaining)
09 if (retval$Success) return(retval)
10 tilesRemaining$pushTail(board[cell])
11 }
12 board[cell] = 0 # Mark this cell as empty
13 # All available tiles for this cell tried without success
14 return( list(Success = FALSE, Board = board) )
15 }
16 success <- evaluateBoard(board)
17 return( list(Success = success, Board = board) )
18 }The function exploits recursion to place each subsequent tile on the next available cell. As there are a maximum of 19 tiles to place, recursion will descend to a maximum of 19 levels (Line 08). The recursion will bottom out when no tiles remain to be placed on the board, and the board will then be evaluated (Line 16). A successful evaluation will immediately unroll the recursion stack (Line 09), propagating the final completed state of the board to the caller (Line 17). An unsuccessful evaluation will recurse one step back up the calling stack and cause the next remaining tile to be tried instead. Once all the tiles are exhausted for a given cell, the recursion will unroll to the previous cell, the next tile in the sequence will be tried, the recursion will progress again, and so on.
Usefully, the placeTiles() function enables us to test a partial solution, so let's try out the partial tile placement from the beginning of this chapter. Execute the following code:
> board <- c(0,19,0,16,3,1,18,0,5,0,4,0,11,7,6,14,0,10,0) > tiles <- sequence() > tiles$pushHead(c(2,8,9,12,13,15,17)) > cells <- c(1,3,8,10,12,17,19) > placeTiles(cells,board,tiles) $Success [1] FALSE $Board [1] 0 19 0 16 3 1 18 0 5 0 4 0 11 7 6 14 0 10 0
Tip
Downloading the example code
You can download the example code files for this book from your account at http://www.packtpub.com. If you purchased this book elsewhere, you can visit http://www.packtpub.com/support and register to have the files e-mailed directly to you.
You can download the code files by following these steps:
Log in or register to our website using your e-mail address and password.
Hover the mouse pointer on the SUPPORT tab at the top.
Click on Code Downloads & Errata.
Enter the name of the book in the Search box.
Select the book for which you're looking to download the code files.
Choose from the drop-down menu where you purchased this book from.
Click on Code Download.
You can also download the code files by clicking on the Code Files button on the book's webpage at the Packt Publishing website. This page can be accessed by entering the book's name in the Search box. Please note that you need to be logged in to your Packt account.
Once the file is downloaded, please make sure that you unzip or extract the folder using the latest version of:
WinRAR / 7-Zip for Windows
Zipeg / iZip / UnRarX for Mac
7-Zip / PeaZip for Linux
The code bundle for the book is also hosted on GitHub at https://github.com/PacktPublishing/repository-name. We also have other code bundles from our rich catalog of books and videos available at https://github.com/PacktPublishing/. Check them out!
Unfortunately, our partial solution does not yield a complete solution.
We'll clearly have to try a lot harder.
Before we jump into parallelizing our solver, let's first examine the efficiency of our current serial implementation. With the existing placeTiles() implementation, the tiles are laid until the board is complete, and then it is evaluated. The partial solution we tested previously, with seven cells unassigned, required 7! = 5,040 calls to evaluateBoard() and a total of 13,699 tile placements.
The most obvious refinement we can make is to test each tile as we place it and check whether the partial solution up to this point is correct rather than waiting until all the tiles are placed. Intuitively, this should significantly reduce the number of tile layouts that we have to explore. Let's implement this change and then compare the difference in performance so that we understand the real benefit from doing this extra implementation work:
cell_lines <- list(
list( c(1,2,3), c(1,4,8), c(1,5,10,15,19) ), #Cell 1
.. # Cell lines 2 to 18 removed for brevity
list( c(12,16,19), c(17,18,19), c(1,5,10,15,19) ) #Cell 19
)
evaluateCell <- function(board,cellplaced)
{
for (lines in cell_lines[cellplaced]) {
for (line in lines) {
total <- 0
checkExact <- TRUE
for (cell in line) {
if (board[cell] == 0) checkExact <- FALSE
else total <- total + board[cell]
}
if ((checkExact && (total != 38)) || total > 38)
return(FALSE)
}
}
return(TRUE)
}For efficiency, the evaluateCell() function determines which lines need to be checked based on the cell that is just placed by performing direct lookup against cell_lines. The cell_lines data structure is easily compiled from all_lines (you could even write some simple code to generate this). Each cell on the board requires three specific lines to be tested. As any given line being tested may not be filled with tiles, evaluateCell() includes a check to ensure that it only applies the 38 sum test when a line is complete. For a partial line, a check is made to ensure that the sum does not exceed 38.
We can now augment placeTiles() to call evaluateCell() as follows:
01 placeTiles <- function(cells,board,tilesRemaining)
..
06 for (t in 1:maxTries) {
07 board[cell] = tilesRemaining$popHead()
++ if (evaluateCell(board,cell)) {
08 retval <- placeTiles(cells,board,tilesRemaining)
09 if (retval$Success) return(retval)
++ }
10 tilesRemaining$pushTail(board[cell])
11 }
..Before we apply this change, we need to first benchmark the current placeTiles() function so that we can determine the resulting performance improvement. To do this, we'll introduce a simple timing function, teval(), that will enable us to measure accurately how much work the processor does when executing a given R function. Take a look at the following:
teval <- function(...) {
gc(); # Perform a garbage collection before timing R function
start <- proc.time()
result <- eval(...)
finish <- proc.time()
return ( list(Duration=finish-start, Result=result) )
}The teval() function makes use of an internal system function, proc.time(), to record the current consumed user and system cycles as well as the wall clock time for the R process [unfortunately, this information is not available when R is running on Windows]. It captures this state both before and after the R expression being measured is evaluated and computes the overall duration. To help ensure that there is a level of consistency in timing, a preemptive garbage collection is invoked, though it should be noted that this does not preclude R from performing a garbage collection at any further point during the timing period.
So, let's run teval() on the existing placeTiles() as follows:
> teval(placeTiles(cells,board,tiles)) $Duration user system elapsed 0.421 0.005 0.519 $Result ..
Now, let's make the changes in placeTiles() to call evaluateCell() and run it again via the following code:
> teval(placeTiles(cells,board,tiles)) $Duration user system elapsed 0.002 0.000 0.002 $Result ..
This is a nice result! This one change has significantly reduced our execution time by a factor of 200. Obviously, your own absolute timings may vary based on the machine you use.
Tip
Benchmarking code
For true comparative benchmarking, we should run tests multiple times and from a full system startup for each run to ensure there are no caching effects or system resource contention issues taking place that might skew our results. For our specific simple example code, which does not perform file I/O or network communications, handle user input, or use large amounts of memory, we should not encounter these issues. Such issues will typically be indicated by significant variation in time taken over multiple runs, a high percentage of system time or the elapsed time being substantively greater than the user + system time.
This kind of performance profiling and enhancement is important as later in this chapter, we will pay directly for our CPU cycles in the cloud; therefore, we want our code to be as cost effective as possible.
For a little deeper understanding of the behavior of our code, such as how many times a function is called during program execution, we either need to add explicit instrumentation, such as counters and print statements, or use external tools such as Rprof. For now, though, we will take a quick look at how we can apply the base R function trace() to provide a generic mechanism to profile the number of times a function is called, as follows:
profileFn <- function(fn) ## Turn on tracing for "fn"
{
assign("profile.counter",0,envir=globalenv())
trace(fn,quote(assign("profile.counter",
get("profile.counter",envir=globalenv()) + 1,
envir=globalenv())), print=FALSE)
}
profileFnStats <- function(fn) ## Get collected stats
{
count <- get("profile.counter",envir=globalenv())
return( list(Function=fn,Count=count) )
}
unprofileFn <- function(fn) ## Turn off tracing and tidy up
{
remove(list="profile.counter",envir=globalenv())
untrace(fn)
}The trace() function enables us to execute a piece of code each time the function being traced is called. We will exploit this to update a specific counter we create (profile.counter) in the global environment to track each invocation.
Note
trace()
This function is only available when the tracing is explicitly compiled into R itself. If you are using the CRAN distribution of R for either Mac OS X or Microsoft Windows, then this facility will be turned on. Tracing introduces a modicum of overhead even when not being used directly within code and therefore tends not to be compiled into R production environments.
We can demonstrate profileFn() working in our running example as follows:
> profile.counter Error: object 'profile.counter' not found > profileFn("evaluateCell") [1] "evaluateCell" > profile.counter [1] 0 > placeTiles(cells,board,tiles) .. > profileFnStats("evaluateCell") $Function [1] "evaluateCell" $Count [1] 59 > unprofileFn("evaluateCell") > profile.counter Error: object 'profile.counter' not found
What this result shows is that evaluateCell() is called 59 times as compared to our previous evaluateBoard() function, which was called 5,096 times. This accounts for the significantly reduced runtime and combinatorial search space that must be explored.
Parallelism relies on being able to split a problem into separate units of work. Trivial—or as it is sometimes referred to, naïve parallelism—treats each separate unit of work as entirely independent of one another. Under this scheme, while a unit of work, or task, is being processed, there is no requirement for the computation to interact with or share information with other tasks being computed, either now, previously, or subsequently.
For our number puzzle, an obvious approach would be to split the problem into 19 separate tasks, where each task is a different-numbered tile placed at cell 1 on the board, and the task is to explore the search space to find a solution stemming from the single tile starting position. However, this only gives us a maximum parallelism of 19, meaning we can explore our search space a maximum of 19 times faster than in serial. We also need to consider our overall efficiency. Does each of the starting positions result in the same amount of required computation? In short, no; as we will use a depth-first algorithm in which a correct solution found will immediately end the task in contrast to an incorrect starting position that will likely result in a much larger, variable, and inevitably fruitless search space being explored. Our tasks are therefore not balanced and will require differing amounts of computational effort to complete. We also cannot predict which of the tasks will take longer to compute as we do not know which starting position will lead to the correct solution a priori.
Note
Imbalanced computation
This type of scenario is typical of a whole host of real-world problems where we search for an optimal or near-optimal solution in a complex search space—for example, finding the most efficient route and means of travel around a set of destinations or planning the most efficient use of human and building resources when timetabling a set of activities. Imbalanced computation can be a significant problem where we have a fully committed compute resource and are effectively waiting for the slowest task to be performed before the overall computation can complete. This reduces our parallel speed-up in comparison to running in serial, and it may also mean that the compute resource we are paying for spends a significant period of time idle rather than doing useful work.
To increase our overall efficiency and opportunity for parallelism, we will split the problem into a larger number of smaller computational tasks, and we will exploit a particular feature of the puzzle to significantly reduce our overall search space.
We will generate the starting triple of tiles for the first (top) line of the board, cells 1 to 3. We might expect that this will give us 19x18x17 = 5,814 tile combinations. However, only a subset of these tile combinations will sum to 38; 1+2+3 and 17+18+19 clearly are not valid. We can also filter out combinations that are a mirror image; for example, for the first line of the board, 1+18+19 will yield an equivalent search space to 19+18+1, so we only need to explore one of them.
Here is the code for generateTriples(). You will notice that we are making use of a 6-character string representation of a tile-triple to simplify the mirror image test, and it also happens to be a reasonably compact and efficient implementation:
generateTriples <- function()
{
triples <- list()
for (x in 1:19) {
for (y in 1:19) {
if (y == x) next
for (z in 1:19) {
if (z == x || z == y || x+y+z != 38) next
mirror <- FALSE
reversed <- sprintf("%02d%02d%02d",z,y,x)
for (t in triples) {
if (reversed == t) {
mirror <- TRUE
break
}
}
if (!mirror) {
triples[length(triples)+1] <-
sprintf("%02d%02d%02d",x,y,z)
}
}
}
}
return (triples)
}If we run this, we will generate just 90 unique triples, a significant saving over 5,814 starting positions:
> teval(generateTriples()) $Duration user system elapsed 0.025 0.001 0.105 $Result[[1]] [1] "011819" .. $Result[[90]] [1] "180119"
Now that we have an efficiently defined set of board starting positions, we can look at how we can manage the set of tasks for distributed computation. Our starting point will be lapply() as this enables us to test out our task execution and formulate it into a program structure, for which we can do a simple drop-in replacement to run in parallel.
The lapply() function takes two arguments, the first is a list of objects that act as input to a user-defined function, and the second is the user-defined function to be called, once for each separate input object; it will return the collection of results from each function invocation as a single list. We will repackage our solver implementation to make it simpler to use with lapply() by wrapping up the various functions and data structures we developed thus far in an overall solver() function, as follows (the complete source code for the solver is available on the book's website):
solver <- function(triple)
{
all_lines <- list(..
cell_lines <- list(..
sequence <- function(..
evaluateBoard <- function(..
evaluateCell <- function(..
placeTiles <- function(..
teval <- function(..
## The main body of the solver
tile1 <- as.integer(substr(triple,1,2))
tile2 <- as.integer(substr(triple,3,4))
tile3 <- as.integer(substr(triple,5,6))
board <- c(tile1,tile2,tile3,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0)
cells <- c(4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19)
tiles <- sequence()
for (t in 1:19) {
if (t == tile1 || t == tile2 || t == tile3) next
tiles$pushHead(t)
}
result <- teval(placeTiles(cells,board,tiles))
return( list(Triple = triple, Result = result$Result,
Duration= result$Duration) )
}Let's run our solver with a selection of four of the tile-triples:
> tri <- generateTriples() > tasks <- list(tri[[1]],tri[[21]],tri[[41]],tri[[61]]) > teval(lapply(tasks,solver)) $Duration ## Overall user system elapsed 171.934 0.216 172.257 $Result[[1]]$Duration ## Triple "011819" user system elapsed 1.113 0.001 1.114 $Result[[2]]$Duration ## Triple "061517" user system elapsed 39.536 0.054 39.615 $Result[[3]]$Duration ## Triple "091019" user system elapsed 65.541 0.089 65.689 $Result[[4]]$Duration ## Triple "111215" user system elapsed 65.609 0.072 65.704
The preceding output has been trimmed and commented for brevity and clarity. The key thing to note is that there is significant variation in the time (the elapsed time) it takes on my laptop to run through the search space for each of the four starting tile-triples, none of which happen to result in a solution to the puzzle. We can (perhaps) project from this that it will take at least 90 minutes to run through the complete set of triples if running in serial. However, we can solve the puzzle much faster if we run our code in parallel; so, without further ado….



