A heap data structure is a specialization of a tree in which the nodes are ordered in a specific way. Heaps are divided into max heaps and min heaps.
In a max heap, each parent node value must always be greater than or equal to its children. It follows that the root node must be the greatest value in the tree. Consider the following diagram for the max heap, where all the nodes have greater values compared to their children:

In a min heap, each parent node must be less than or equal to both its children. As a consequence, the root node holds the lowest value. Consider the following diagram for the min heap, where all the nodes have smaller values compared to their children:
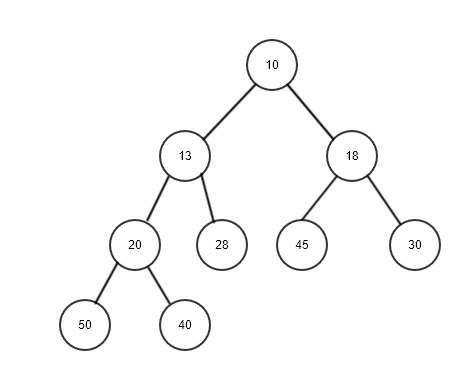
Heaps are used for a number of different things. For one, they are used to implement priority queues. There is also a very efficient sorting algorithm, called heap sort, that uses heaps. We are going...



