In the first step, we generate a simple toy time series. The series consists of values on a line sprinkled with some added noise. Next, we plot our time series in step 2. You can see that it is very close to a straight line and that a sensible prediction for the value of the time series at time  is
is  . To create a forecast of the value of the time series, we consider three different schemes (step 3) for predicting the future values of the time series. In an autoregressive model, the basic idea is that the value of the time series at time t is a linear function of the values of the time series at the previous times. More precisely, there are some constants,
. To create a forecast of the value of the time series, we consider three different schemes (step 3) for predicting the future values of the time series. In an autoregressive model, the basic idea is that the value of the time series at time t is a linear function of the values of the time series at the previous times. More precisely, there are some constants,  , and a number,
, and a number,  , such that:
, such that:

As a hypothetical example,  may be 3, meaning that the value of the time series can be easily computed from knowing its last 3 values.
may be 3, meaning that the value of the time series can be easily computed from knowing its last 3 values.
In the moving-average model, the time series is modeled as fluctuating about a mean. More precisely, let  be a sequence of i.i.d normal variables and let
be a sequence of i.i.d normal variables and let  be a constant. Then, the time series is modeled by the following formula:
be a constant. Then, the time series is modeled by the following formula:
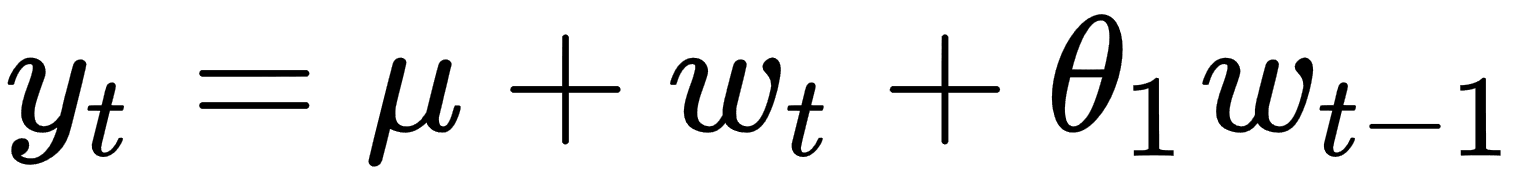
For that reason, it performs poorly in predicting the noisy linear time series we have generated.
Finally, in simple exponential smoothing, we propose a smoothing parameter,  . Then, our model's estimate,
. Then, our model's estimate,  , is computed from the following equations:
, is computed from the following equations:
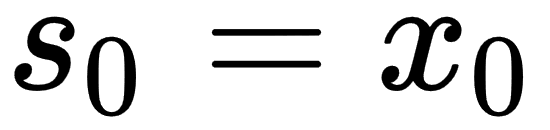
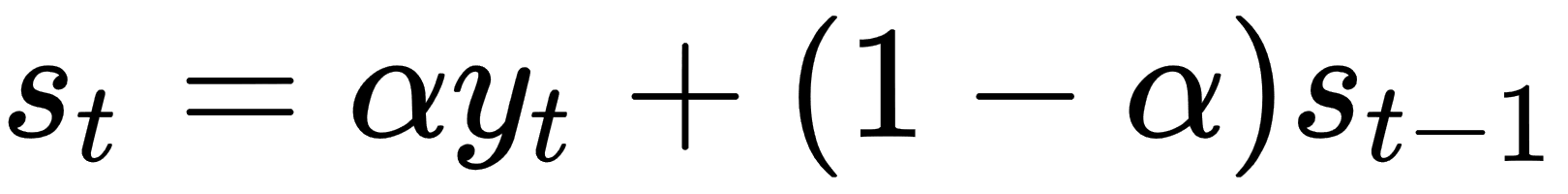
In other words, we keep track of an estimate,  , and adjust it slightly using the current time series value,
, and adjust it slightly using the current time series value,  . How strongly the adjustment is made is regulated by the
. How strongly the adjustment is made is regulated by the  parameter.
parameter.






 is
is  . To create a forecast of the value of the time series, we consider three different schemes (step 3) for predicting the future values of the time series. In an autoregressive model, the basic idea is that the value of the time series at time t is a linear function of the values of the time series at the previous times. More precisely, there are some constants,
. To create a forecast of the value of the time series, we consider three different schemes (step 3) for predicting the future values of the time series. In an autoregressive model, the basic idea is that the value of the time series at time t is a linear function of the values of the time series at the previous times. More precisely, there are some constants,  , and a number,
, and a number,  , such that:
, such that:
 may be 3, meaning that the value of the time series can be easily computed from knowing its last 3 values.
may be 3, meaning that the value of the time series can be easily computed from knowing its last 3 values. be a sequence of i.i.d normal variables and let
be a sequence of i.i.d normal variables and let  be a constant. Then, the time series is modeled by the following formula:
be a constant. Then, the time series is modeled by the following formula: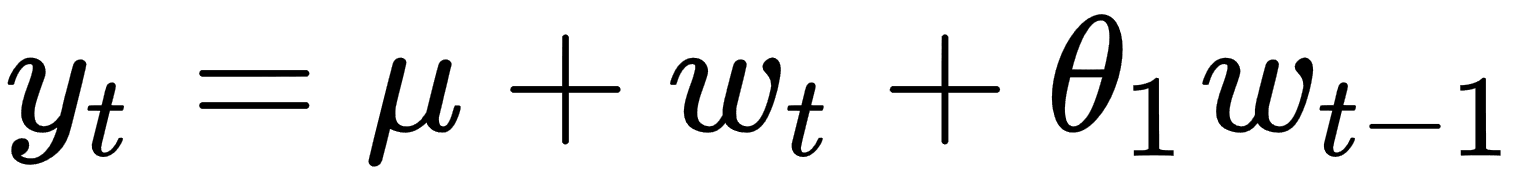
 . Then, our model's estimate,
. Then, our model's estimate,  , is computed from the following equations:
, is computed from the following equations: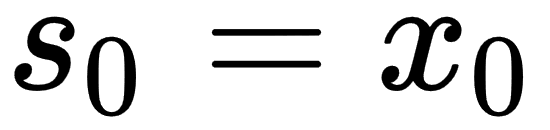
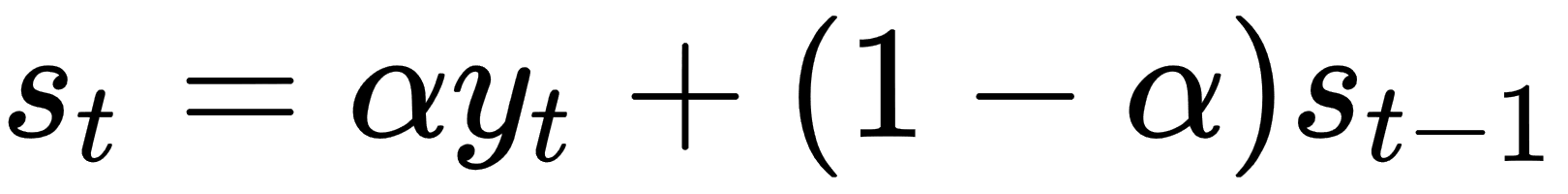
 , and adjust it slightly using the current time series value,
, and adjust it slightly using the current time series value,  . How strongly the adjustment is made is regulated by the
. How strongly the adjustment is made is regulated by the 