Introduction to GWR models
GWR models vary from OLS-based models in that instead of fitting a set of global estimates, GWR examines the way in which the relationship between each predictor variable varies across space with respect to the dependent variable. GWR does this by iteratively fitting a localized regression within a search window or neighborhood around each observation. The observation for which the regression is being fit is known as the regression point. Observations that are closer to the regression point are weighted more heavily in the regression than observations that are further away.
Fitting a regression within these local neighborhoods is performed by using either a fixed kernel or an adaptive kernel. A fixed kernel uses an identical search area across all regression points, while an adaptive kernel’s search area can vary across space. Figure 9.11 shows a fixed kernel approach compared to an adaptive kernel approach.
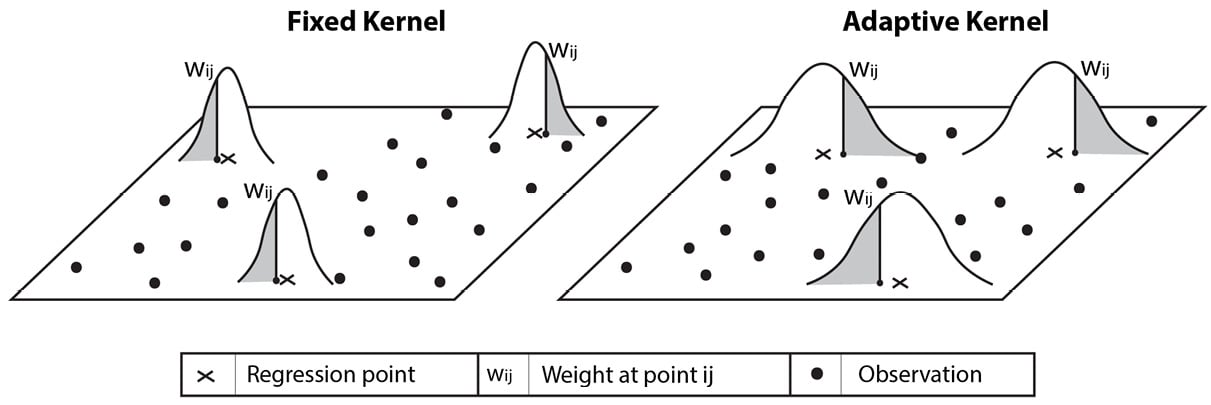
Figure 9.11...



