Book Image

Data Science Using Python and R

By : Chantal D. Larose, Daniel T. Larose
Book Image

Data Science Using Python and R

By: Chantal D. Larose, Daniel T. Larose

Overview of this book

Data science is hot. Bloomberg named a data scientist as the ‘hottest job in America’. Python and R are the top two open-source data science tools using which you can produce hands-on solutions to real-world business problems, using state-of-the-art techniques. Each chapter in the book presents step-by-step instructions and walkthroughs for solving data science problems using Python and R. You’ll learn how to prepare data, perform exploratory data analysis, and prepare to model the data. As you progress, you’ll explore what are decision trees and how to use them. You’ll also learn about model evaluation, misclassification costs, naïve Bayes classification, and neural networks. The later chapters provide comprehensive information about clustering, regression modeling, dimension reduction, and association rules mining. The book also throws light on exciting new topics, such as random forests and general linear models. The book emphasizes data-driven error costs to enhance profitability, which avoids the common pitfalls that may cost a company millions of dollars. By the end of this book, you’ll have enough knowledge and confidence to start providing solutions to data science problems using R and Python.

Related Content you might be interested in

Current Title:

Small book image
Data Science Using Python and R
Chantal D. Larose | Daniel T. Larose
Apr, 2019 | 256 pages
Small book image
Business Intelligence Career Master Plan
Danny Moncada | Eduardo Chavez
Aug, 2023 | 284 pages
Small book image
Mastering NLP from Foundations to LLMs
Meysam Ghaffari | Lior Gazit
Apr, 2024 | 340 pages
Small book image
Principles of Data Science
Sinan Ozdemir
Jan, 2024 | 326 pages
Table of Contents (20 chapters)
PREFACEBegin Reading
PREFACEBegin Reading
DATA SCIENCE USING PYTHON AND R
Free Chapter
1
ABOUT THE AUTHORS
ABOUT THE AUTHORS
2
ACKNOWLEDGMENTS
CHANTAL'S ACKNOWLEDGMENTS
DANIEL'S ACKNOWLEDGMENTS
3
Chapter 1: INTRODUCTION TO DATA SCIENCE
Chapter 1: INTRODUCTION TO DATA SCIENCE
1.1 WHY DATA SCIENCE?
1.2 WHAT IS DATA SCIENCE?
1.3 THE DATA SCIENCE METHODOLOGY
1.4 DATA SCIENCE TASKS
EXERCISES
4
Chapter 2: THE BASICS OF PYTHON AND R
Chapter 2: THE BASICS OF PYTHON AND R
2.1 DOWNLOADING PYTHON
2.2 BASICS OF CODING IN PYTHON
2.3 DOWNLOADING R AND RSTUDIO
2.4 BASICS OF CODING IN R
REFERENCES
EXERCISES
5
Chapter 3: DATA PREPARATION
Chapter 3: DATA PREPARATION
3.1 THE BANK MARKETING DATA SET
3.2 THE PROBLEM UNDERSTANDING PHASE
3.3 DATA PREPARATION PHASE
3.4 ADDING AN INDEX FIELD
3.5 CHANGING MISLEADING FIELD VALUES
3.6 REEXPRESSION OF CATEGORICAL DATA AS NUMERIC
3.7 STANDARDIZING THE NUMERIC FIELDS
3.8 IDENTIFYING OUTLIERS
REFERENCES
EXERCISES
6
Chapter 4: EXPLORATORY DATA ANALYSIS
Chapter 4: EXPLORATORY DATA ANALYSIS
4.1 EDA VERSUS HT
4.2 BAR GRAPHS WITH RESPONSE OVERLAY
4.3 CONTINGENCY TABLES
4.4 HISTOGRAMS WITH RESPONSE OVERLAY
4.5 BINNING BASED ON PREDICTIVE VALUE
REFERENCES
EXERCISES
7
Chapter 5: PREPARING TO MODEL THE DATA
Chapter 5: PREPARING TO MODEL THE DATA
5.1 THE STORY SO FAR
5.2 PARTITIONING THE DATA
5.3 VALIDATING YOUR PARTITION
5.4 BALANCING THE TRAINING DATA SET
5.5 ESTABLISHING BASELINE MODEL PERFORMANCE
REFERENCES
EXERCISES
8
Chapter 6: DECISION TREES
Chapter 6: DECISION TREES
6.1 INTRODUCTION TO DECISION TREES
6.2 CLASSIFICATION AND REGRESSION TREES
6.3 THE C5.0 ALGORITHM FOR BUILDING DECISION TREES
6.4 RANDOM FORESTS
REFERENCES
EXERCISES
9
Chapter 7: MODEL EVALUATION
Chapter 7: MODEL EVALUATION
7.1 INTRODUCTION TO MODEL EVALUATION
7.2 CLASSIFICATION EVALUATION MEASURES
7.3 SENSITIVITY AND SPECIFICITY
7.4 PRECISION, RECALL, AND Fβ SCORES
7.5 METHOD FOR MODEL EVALUATION
7.6 AN APPLICATION OF MODEL EVALUATION
7.7 ACCOUNTING FOR UNEQUAL ERROR COSTS
7.8 COMPARING MODELS WITH AND WITHOUT UNEQUAL ERROR COSTS
7.9 DATA‐DRIVEN ERROR COSTS
EXERCISES
10
Chapter 8: NAÏVE BAYES CLASSIFICATION
Chapter 8: NAÏVE BAYES CLASSIFICATION
8.1 INTRODUCTION TO NAÏVE BAYES
8.2 BAYES THEOREM
8.3 MAXIMUM A POSTERIORI HYPOTHESIS
8.4 CLASS CONDITIONAL INDEPENDENCE
8.5 APPLICATION OF NAÏVE BAYES CLASSIFICATION
REFERENCES
EXERCISES
11
Chapter 9: NEURAL NETWORKS
Chapter 9: NEURAL NETWORKS
9.1 INTRODUCTION TO NEURAL NETWORKS
9.2 THE NEURAL NETWORK STRUCTURE
9.3 CONNECTION WEIGHTS AND THE COMBINATION FUNCTION
9.4 THE SIGMOID ACTIVATION FUNCTION
9.5 BACKPROPAGATION
9.6 AN APPLICATION OF A NEURAL NETWORK MODEL
9.7 INTERPRETING THE WEIGHTS IN A NEURAL NETWORK MODEL
9.8 HOW TO USE NEURAL NETWORKS IN R
REFERENCES
EXERCISES
12
Chapter 10: CLUSTERING
Chapter 10: CLUSTERING
10.1 WHAT IS CLUSTERING?
10.2 INTRODUCTION TO THE k‐MEANS CLUSTERING ALGORITHM
10.3 AN APPLICATION OF k‐MEANS CLUSTERING
10.4 CLUSTER VALIDATION
10.5 HOW TO PERFORM k‐MEANS CLUSTERING USING PYTHON
10.6 HOW TO PERFORM k‐MEANS CLUSTERING USING R
EXERCISES
13
Chapter 11: REGRESSION MODELING
Chapter 11: REGRESSION MODELING
11.1 THE ESTIMATION TASK
11.2 DESCRIPTIVE REGRESSION MODELING
11.3 AN APPLICATION OF MULTIPLE REGRESSION MODELING
11.4 HOW TO PERFORM MULTIPLE REGRESSION MODELING USING PYTHON
11.5 HOW TO PERFORM MULTIPLE REGRESSION MODELING USING R
11.6 MODEL EVALUATION FOR ESTIMATION
11.7 STEPWISE REGRESSION
11.8 BASELINE MODELS FOR REGRESSION
REFERENCES
EXERCISES
14
Chapter 12: DIMENSION REDUCTION
Chapter 12: DIMENSION REDUCTION
12.1 THE NEED FOR DIMENSION REDUCTION
12.2 MULTICOLLINEARITY
12.3 IDENTIFYING MULTICOLLINEARITY USING VARIANCE INFLATION FACTORS
12.4 PRINCIPAL COMPONENTS ANALYSIS
12.5 AN APPLICATION OF PRINCIPAL COMPONENTS ANALYSIS
12.6 HOW MANY COMPONENTS SHOULD WE EXTRACT?
12.7 PERFORMING PCA WITH k = 4
12.8 VALIDATION OF THE PRINCIPAL COMPONENTS
12.9 HOW TO PERFORM PRINCIPAL COMPONENTS ANALYSIS USING PYTHON
12.10 HOW TO PERFORM PRINCIPAL COMPONENTS ANALYSIS USING R
12.11 WHEN IS MULTICOLLINEARITY NOT A PROBLEM?
REFERENCES
EXERCISES
15
Chapter 13: GENERALIZED LINEAR MODELS
Chapter 13: GENERALIZED LINEAR MODELS
13.1 AN OVERVIEW OF GENERAL LINEAR MODELS
13.2 LINEAR REGRESSION AS A GENERAL LINEAR MODEL
13.3 LOGISTIC REGRESSION AS A GENERAL LINEAR MODEL
13.4 AN APPLICATION OF LOGISTIC REGRESSION MODELING
13.5 POISSON REGRESSION
13.6 AN APPLICATION OF POISSON REGRESSION MODELING
REFERENCE
EXERCISES
16
Chapter 14: ASSOCIATION RULES
Chapter 14: ASSOCIATION RULES
14.1 INTRODUCTION TO ASSOCIATION RULES
14.2 A SIMPLE EXAMPLE OF ASSOCIATION RULE MINING
14.3 SUPPORT, CONFIDENCE, AND LIFT
14.4 MINING ASSOCIATION RULES
14.5 CONFIRMING OUR METRICS
14.6 THE CONFIDENCE DIFFERENCE CRITERION
14.7 THE CONFIDENCE QUOTIENT CRITERION
REFERENCES
EXERCISES
17
INDEX
INDEX
18
END USER LICENSE AGREEMENT
END USER LICENSE AGREEMENT
APPENDIX DATA SUMMARIZATION AND VISUALIZATION
APPENDIX DATA SUMMARIZATION AND VISUALIZATION
PART 1: SUMMARIZATION 1: BUILDING BLOCKS OF DATA ANALYSIS
PART 2: VISUALIZATION: GRAPHS AND TABLES FOR SUMMARIZING AND ORGANIZING DATA
PART 3: SUMMARIZATION 2: MEASURES OF CENTER, VARIABILITY, AND POSITION
PART 4: SUMMARIZATION AND VISUALIZATION OF BIVARIATE RELATIONSHIPS

9.3 CONNECTION WEIGHTS AND THE COMBINATION FUNCTION

The nodes in the hidden layer and the output layer collect the inputs from the previous layer and combine them using a combination function. This combination function (usually summation, Σ) produces a linear combination of the node inputs and the connection weights into a single scalar value, which we will term net. Thus, for a given node j,

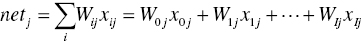
equationnetj=∑iWijxij=W0jx0j+W1jx1j+⋯+WIjxIj--

where xij represents the ith input to node j, Wij represents the weight associated with the ith input to node j, and there are I + 1 inputs to node j. Note that x1, x2, …, xI represent inputs from upstream nodes, while x0 represents a constant input, analogous to the constant factor in regression models, which by convention uniquely takes the value x0j = 1. Thus, each hidden layer or output layer node j contains an “extra” input equal to a particular weight W0j x0j = W0j, such as W0B for node B.

We...

Previous Section
End of Section 4
Next Section