One of the most well-known reinforcement learning techniques, and the one we will be implementing in our example, is Q-learning.
Q-learning can be used to find an optimal action for any given state in a finite Markov decision process. Q-learning tries to maximize the value of the Q-function that represents the maximum discounted future reward when we perform action a in state s.
Once we know the Q-function, the optimal action a in state s is the one with the highest Q-value. We can then define a policy π(s), that gives us the optimal action in any state, expressed as follows:
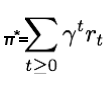
We can define the Q-function for a transition point (st, at, rt, st+1) in terms of the Q-function at the next point (st+1, at+1, rt+1, st+2), similar to what we did with the total discounted future reward. This equation is known as the Bellman equation for Q-learning...


