In the previous section, we gave an introduction to MDP. In this section, we will define the problem statement formally and see the algorithms for solving it.
An MDP is used to define the environment in reinforcement learning and almost all reinforcement learning problems can be defined using an MDP.
For understanding MDPs we need to use the concept of the Markov reward process (MRP). An MRP is a stochastic process which extends a Markov chain by adding a reward rate to each state. We can also define an additional variable to keep a track of the accumulated reward over time. Formally, an MRP is defined by  where S is a finite state space, P is the state transition probability function, R is a reward function, and
where S is a finite state space, P is the state transition probability function, R is a reward function, and 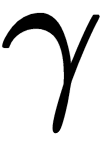 is the discount rate:
is the discount rate:
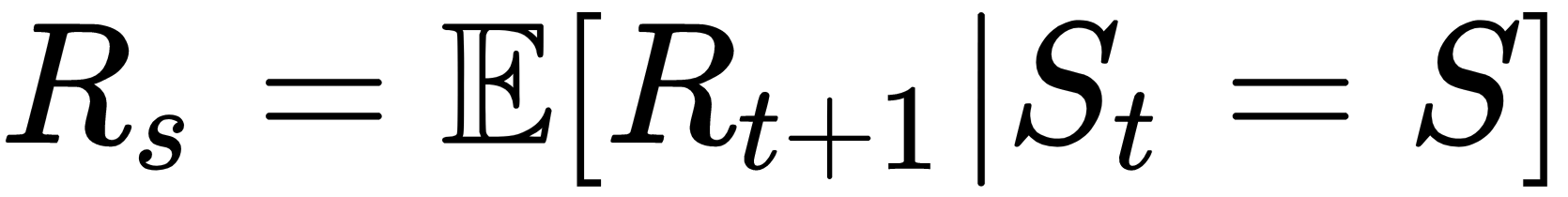
where  denotes the expectation. And the term Rs here denotes the expected reward at the state s.
denotes the expectation. And the term Rs here denotes the expected reward at the state s.
In the case of...



