Scroll to the empty cells at the bottom of Subtopic C in your Jupyter Notebook.

These will be found beneath the linear-model MSE calculation cell under the Activity heading.

We will first pull out our dependent feature from and target variable from df. using the following:

y = df['MEDV'].values
x = df['LSTAT'].values.reshape(-1,1)

This is identical to what we did earlier for the linear model.

Verify what x looks like by printing the first few samples with print(x[:3]):

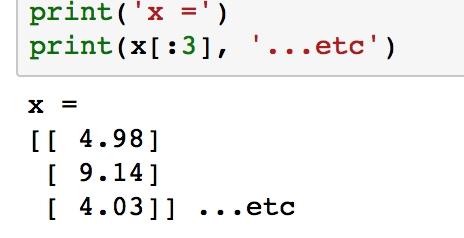
Figure 1.49: Printing first three values of x using print()

Notice how each element in the array is itself an array with length 1. This is what reshape(-1,1) does, and it is the form expected by scikit-learn.

Transform x into "polynomial features" by importing the appropriate transformation tool from scikit-learn and instantiating the third-degree polynomial feature transformer:

from sklearn.preprocessing import PolynomialFeatures poly = PolynomialFeatures(degree=3)

The rationale for this step may not be immediately obvious but will be explained shortly.

Transform the LSTAT feature (as stored in the variable x) by running the fit_transform method. Build the polynomial feature set by running the following code:

x_poly = poly.fit_transform(x)

Here, we have used the instance of the transformer feature to transform the LSTAT variable.

Verify what x_poly looks like by printing the first few samples with print(x_poly[:3]).

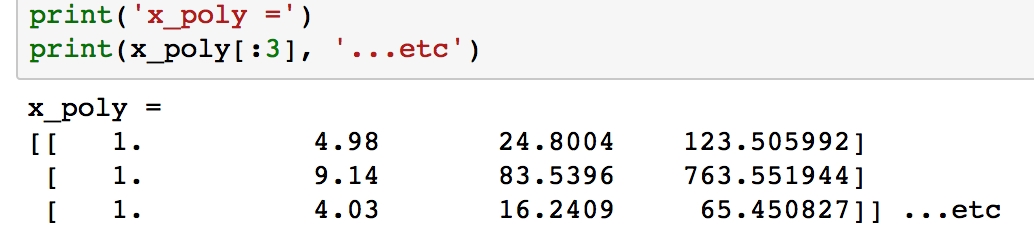
Figure 1.50: Printing first three values of x_poly using print()

Unlike x, the arrays in each row now have length 4, where the values have been calculated as xº, x¹, x² and x³.

We are now going to use this data to fit a linear model. Labeling the features as a, b, c, and d, we will calculate the coefficients α0, α1, α2, and α3 and of the linear model:

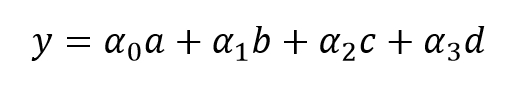
We can plug in the definitions of a, b, c, and d, to get the following polynomial model, where the coefficients are the same as the previous ones:

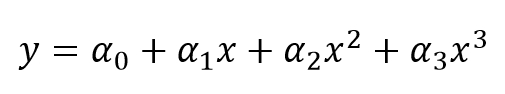
Import the LinearRegression class and build our linear classification model the same way as done while calculating the MSE. Run the following:

from sklearn.linear_model import LinearRegression clf = 
LinearRegression()
clf.fit(x_poly, y)

Extract the coefficients and print the polynomial model using the following code:

a_0 = clf.intercept_ + clf.coef_[0] # intercepta_1, a_2, a_3 = clf.coef_[1:]       # other coefficients

msg = 'model: y = {:.3f} + {:.3f}x + {:.3f}x^2 + {:.3f}x^3'\.format(a_0, a_1, a_2, a_3)print(msg)

Figure 1.51: Extracting coefficients and printing the polynomial model

To get the actual model intercept, we have to add the intercept_ and coef_

[0] attributes. The higher-order coefficients are then given by the remaining values of coef_.

Determine the predicted values for each sample and calculate the residuals by running the following code:

y_pred = clf.predict(x_poly) resid_MEDV = y - y_pred

Print some of the residual values by running print(resid_MEDV[:10]):

Figure 1.52: Printing residual values

We'll plot these soon to compare with the linear model residuals, but first we will calculate the MSE.

Run the following code to print the MSE for the third-order polynomial model:

from sklearn.metrics import mean_squared_error error = mean_squared_error(y, y_pred) print('mse = {:.2f}'.format(error))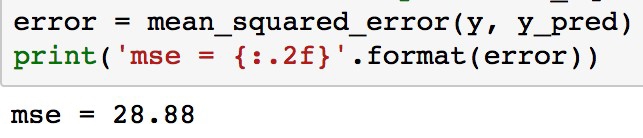

Figure 1.53: Calculating the mean squared error

As can be seen, the MSE is significantly less for the polynomial model compared to the linear model (which was 38.5). This error metric can be converted to an average error in dollars by taking the square root. Doing this for the polynomial model, we find the average error for the median house value is only $5,300.

Now, we'll visualize the model by plotting the polynomial line of best fit along with the data.

Plot the polynomial model along with the samples by running the following:

fig, ax = plt.subplots() # Plot the samples
ax.scatter(x.flatten(), y, alpha=0.6)
# Plot the polynomial model
x_ = np.linspace(2, 38, 50).reshape(-1, 1) x_poly = poly.fit_transform(x_)
y_ = clf.predict(x_poly)
ax.plot(x_, y_, color='red', alpha=0.8) ax.set_xlabel('LSTAT'); ax.set_ylabel('MEDV');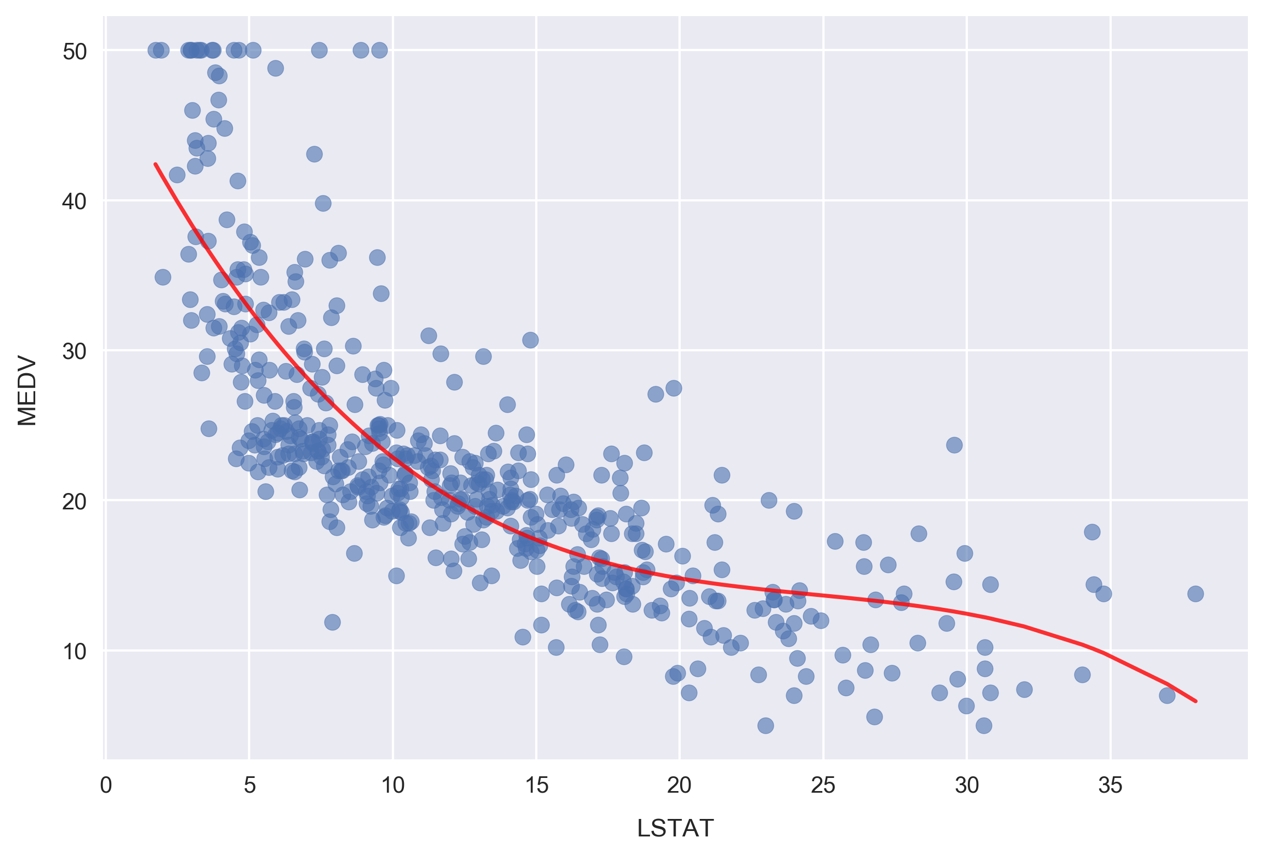

Figure 1.54: Plotting the polynomial model for MEDV and LSTAT

Here, we are plotting the red curve by calculating the polynomial model predictions on an array of x values. The array of x values was created using np.linspace, resulting in 50 values arranged evenly between 2 and 38.

Now, we'll plot the corresponding residuals. Whereas we used Seaborn for this earlier, we'll have to do it manually to show results for a scikit-learn model. Since we already calculated the residuals earlier, as reference by the resid_MEDV variable, we simply need to plot this list of values on a scatter chart.

Plot the residuals by running the following:

fig, ax = plt.subplots(figsize=(5, 7)) ax.scatter(x, resid_MEDV, alpha=0.6) ax.set_xlabel('LSTAT')
ax.set_ylabel('MEDV Residual $(y-\hat{y})$') plt.axhline(0, color='black', ls='dotted');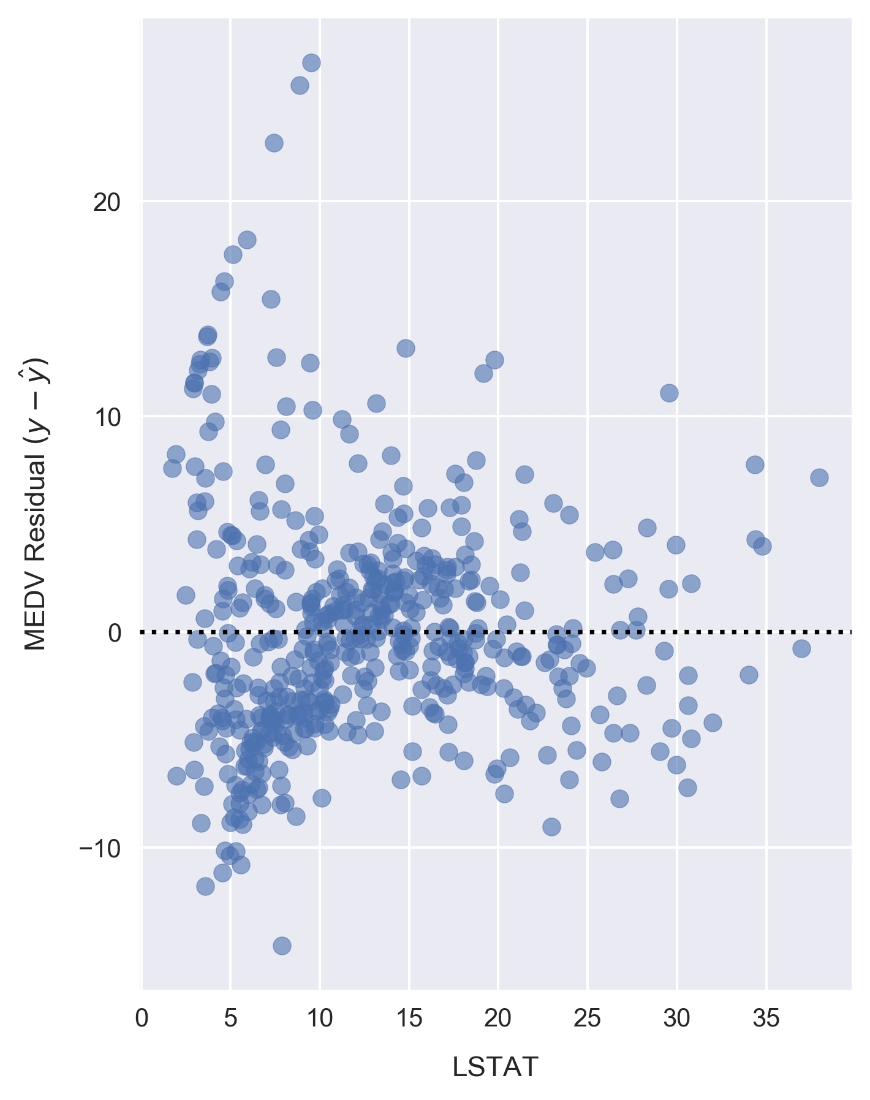

Figure 1.55: Plotting the residuals for LSTAT and MEDV

Compared to the linear model LSTAT residual plot, the polynomial model residuals appear to be more closely clustered around y - ŷ = 0. Note that y is the sample MEDV and ŷ is the predicted value. There are still clear patterns, such as the cluster near x = 7 and y = -7 that indicates suboptimal modeling.