Why graph learning?

Graph learning is the application of machine learning techniques to graph data. This study area encompasses a range of tasks aimed at understanding and manipulating graph-structured data. There are many graphs learning tasks, including the following:

• Node classification is a task that involves predicting the category (class) of a node in a graph. For example, it can categorize online users or items based on their characteristics. In this task, the model is trained on a set of labeled nodes and their attributes, and it uses this information to predict the class of unlabeled nodes.
• Link prediction is a task that involves predicting missing links between pairs of nodes in a graph. This is useful in knowledge graph completion, where the goal is to complete a graph of entities and their relationships. For example, it can be used to predict the relationships between people based on their social network connections (friend recommendation).
• Graph classification is a task that involves categorizing different graphs into predefined categories. One example of this is in molecular biology, where molecular structures can be represented as graphs, and the goal is to predict their properties for drug design. In this task, the model is trained on a set of labeled graphs and their attributes, and it uses this information to categorize unseen graphs.
• Graph generation is a task that involves generating new graphs based on a set of desired properties. One of the main applications is generating novel molecular structures for drug discovery. This is achieved by training a model on a set of existing molecular structures and then using it to generate new, unseen structures. The generated structures can be evaluated for their potential as drug candidates and further studied.

Graph learning has many other practical applications that can have a significant impact. One of the most well-known applications is recommender systems, where graph learning algorithms recommend relevant items to users based on their previous interactions and relationships with other items. Another important application is traffic forecasting, where graph learning can improve travel time predictions by considering the complex relationships between different routes and modes of transportation.

The versatility and potential of graph learning make it an exciting field of research and development. The study of graphs has advanced rapidly in recent years, driven by the availability of large datasets, powerful computing resources, and advancements in machine learning and artificial intelligence. As a result, we can list four prominent families of graph learning techniques [1]:

• Graph signal processing, which applies traditional signal processing methods to graphs, such as the graph Fourier transform and spectral analysis. These techniques reveal the intrinsic properties of the graph, such as its connectivity and structure.
• Matrix factorization, which seeks to find low-dimensional representations of large matrices. The goal of matrix factorization is to identify latent factors or patterns that explain the observed relationships in the original matrix. This approach can provide a compact and interpretable representation of the data.
• Random walk, which refers to a mathematical concept used to model the movement of entities in a graph. By simulating random walks over a graph, information about the relationships between nodes can be gathered. This is why they are often used to generate training data for machine learning models.
• Deep learning, which is a subfield of machine learning that focuses on neural networks with multiple layers. Deep learning methods can effectively encode and represent graph data as vectors. These vectors can then be used in various tasks with remarkable performance.

It is important to note that these techniques are not mutually exclusive and often overlap in their applications. In practice, they are often combined to form hybrid models that leverage the strengths of each. For example, matrix factorization and deep learning techniques might be used in combination to learn low-dimensional representations of graph-structured data.

As we delve into the world of graph learning, it is crucial to understand the fundamental building block of any machine learning technique: the dataset. Traditional tabular datasets, such as spreadsheets, represent data as rows and columns with each row representing a single data point. However, in many real-world scenarios, the relationships between data points are just as meaningful as the data points themselves. This is where graph datasets come in. Graph datasets represent data points as nodes in a graph and the relationships between those data points as edges.

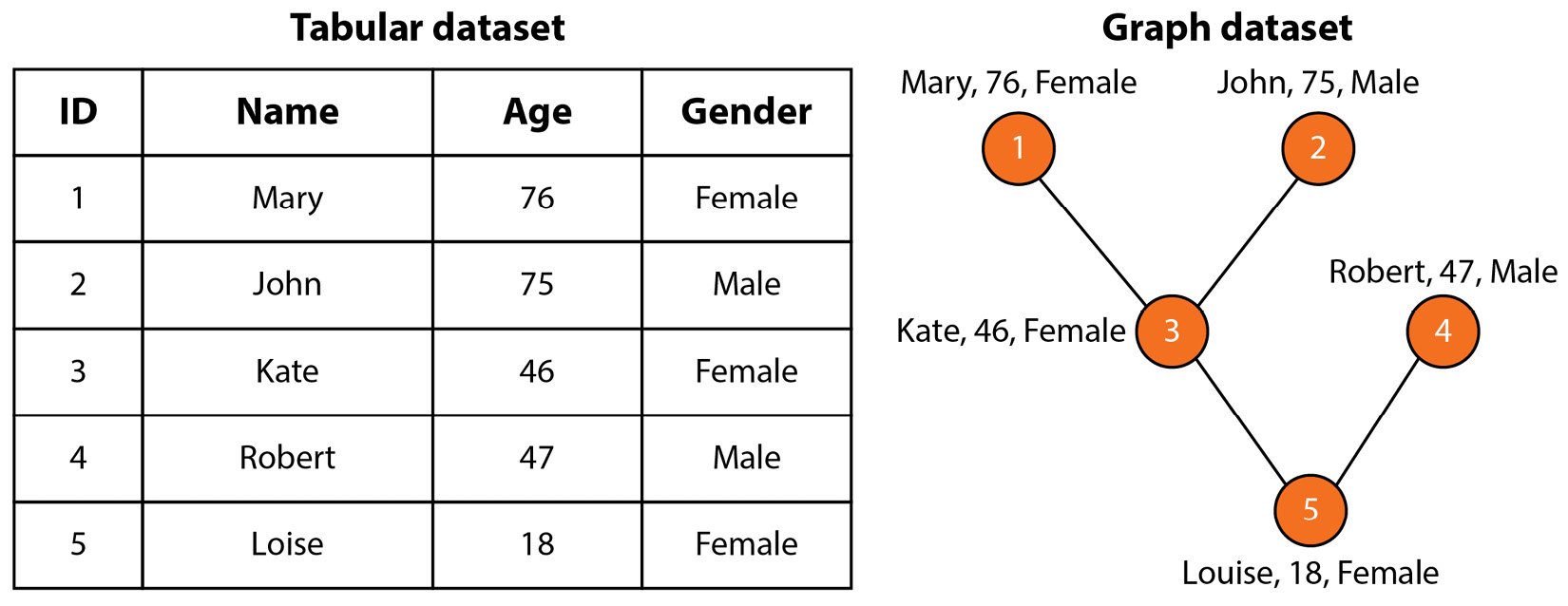
Let’s take the tabular dataset shown in Figure 1.3 as an example.

Figure 1.3 – Family tree as a tabular dataset versus a graph dataset

This dataset represents information about five members of a family. Each member has three features (or attributes): name, age, and gender. However, the tabular version of this dataset doesn’t show the connections between these people. On the contrary, the graph version represents them with edges, which allows us to understand the relationships in this family. In many contexts, the connections between nodes are crucial in understanding the data, which is why representing data in graph form is becoming increasingly popular.

Now that we have a basic understanding of graph machine learning and the different types of tasks it involves, we can move on to exploring one of the most important approaches for solving these tasks: graph neural networks.