Solving equations
Many mathematical problems eventually reduce to solving an equation of the form 
, where 
is a function of a single variable. Here, we try to find a value of 
for which the equation holds. The values of 
for which the equation holds are sometimes called roots of the equation. There are numerous algorithms for finding solutions to equations of this form. In this recipe, we will use the Newton-Raphson and secant methods to solve an equation of the form 
.
The Newton-Raphson method (Newton’s method) and the secant method are good, standard root-finding algorithms that can be applied in almost any situation. These are iterative methods that start with an approximation of the root and iteratively improve this approximation until it lies within a given tolerance.
To demonstrate these techniques, we will use the function from the Differentiating and integrating symbolically using SymPy recipe, defined by the following formula:
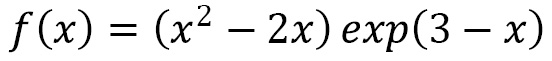
This is...