Chapter 3: Feature Engineering

Activity 10: Calculating Time series Feature – Binning

Solution:

1. Load the caret library:

   #Time series features

   library(caret)

   #Install caret if not installed

   #install.packages('caret')

2. Load the GermanCredit dataset:

   GermanCredit = read.csv("GermanCredit.csv")

   duration<- GermanCredit$Duration #take the duration column

3. Check the data summary as follows:

   summary(duration)

   The output is as follows:

   

   Figure 3.27: The summary of the Duration values of German Credit dataset

4. Load the ggplot2 library:

   library(ggplot2)

5. Plot using the command:

   ggplot(data=GermanCredit, aes(x=GermanCredit$Duration)) +

     geom_density(fill='lightblue') +

     geom_rug() +

     labs(x='mean Duration')

   The output is as follows:

   

   Figure 3.28: Plot of the duration vs density

6. Create bins:

   #Creating Bins

   # set up boundaries for intervals/bins

   breaks <- c(0,10,20,30,40,50,60,70,80)

7. Create labels:

   # specify interval/bin labels

   labels <- c("<10", "10-20", "20-30", "30-40", "40-50", "50-60", "60-70", "70-80")

8. Bucket the datapoints into the bins.

   # bucketing data points into bins

   bins <- cut(duration, breaks, include.lowest = T, right=FALSE, labels=labels)

9. Find the number of elements in each bin:

   # inspect bins

   summary(bins)

   The output is as follows:

   summary(bins)

     <10 10-20 20-30 30-40 40-50 50-60 60-70 70-80

     143   403   241   131    66     2    13     1

10. Plot the bins:

    #Ploting the bins

    plot(bins, main="Frequency of Duration", ylab="Duration Count", xlab="Duration Bins",col="bisque")

    The output is as follows:

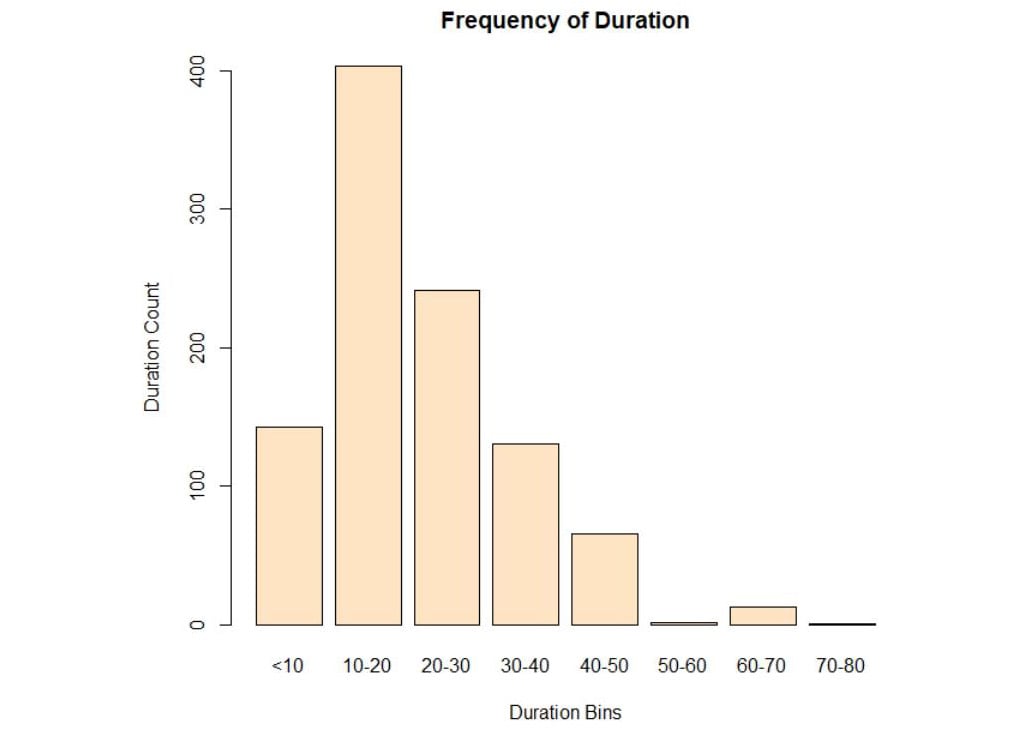
Figure 3.29: Plot of duration in bins

We can conclude that the maximum number of customers are within the range of 10 to 20.

Activity 11: Identifying Skewness

Solution:

1. Load the library mlbench.

   #Skewness

   library(mlbench)

   library(e1071)

2. Load the PrimaIndainsDiabetes data.

   PimaIndiansDiabetes = read.csv("PimaIndiansDiabetes.csv")

3. Print the skewness of the glucose column, using the skewness() function.

   #Printing the skewness of the columns

   #Not skewed

   skewness(PimaIndiansDiabetes$glucose)

   The output is as follows:

   [1] 0.1730754

4. Plot the histogram using the histogram() function.

   histogram(PimaIndiansDiabetes$glucose)

   The output is as follows:

   

   Figure 3.30: Histogram of the glucose values of the PrimaIndainsGlucose dataset

   A negative skewness value means that the data is skewed to the left and a positive skewness value means that the data is skewed to the right. Since the value here is 0.17, the data is neither completely left or right skewed. Therefore, it is not skewed.

5. Find the skewness of the age column using the skewness() function.

   #Highly skewed

   skewness(PimaIndiansDiabetes$age)

   The output is as follows:

   [1] 1.125188

6. Plot the histogram using the histogram() function.

   histogram(PimaIndiansDiabetes$age)

   The output is as follows:

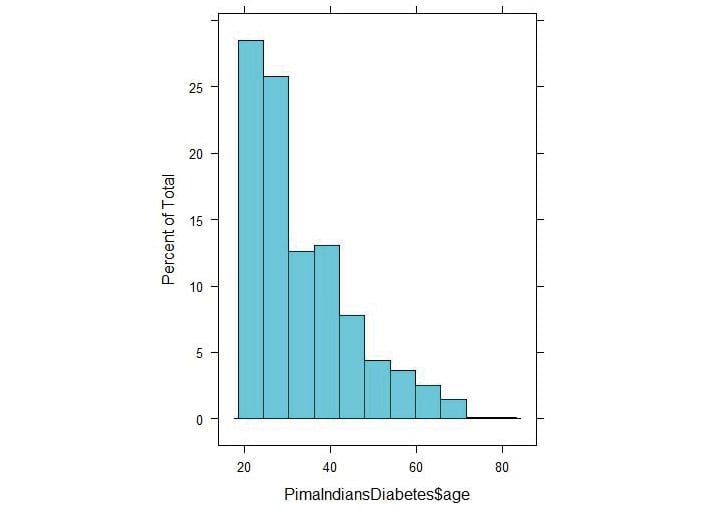
Figure 3.31: Histogram of the age values of the PrimaIndiansDiabetes dataset

The positive skewness value means that it is skewed to the right as we can see above.

Activity 12: Generating PCA

Solution:

1. Load the GermanCredit data.

   #PCA Analysis

   data(GermanCredit)

2. Create a subset of first 9 columns into another variable names GermanCredit_subset

   #Use the German Credit Data

   GermanCredit_subset <- GermanCredit[,1:9]

3. Find the principal components:

   #Find out the Principal components

   principal_components <- prcomp(x = GermanCredit_subset, scale. = T)

4. Print the principal components:

   #Print the principal components

   print(principal_components)

   The output is as follows:

   Standard deviations (1, .., p=9):

   [1] 1.3505916 1.2008442 1.1084157 0.9721503 0.9459586

   0.9317018 0.9106746 0.8345178 0.5211137

   Rotation (n x k) = (9 x 9):

Figure 3.32: Histogram of the age values of the PrimaIndiansDiabetes dataset

Therefore, by using principal component analysis we can identify the top nine principal components in the dataset. These components are calculated from multiple fields and they can be used as features on their own.

Activity 13: Implementing the Random Forest Approach

Solution:

1. Load the GermanCredit data:

   data(GermanCredit)

2. Create a subset to load the first ten columns into GermanCredit_subset.

   GermanCredit_subset <- GermanCredit[,1:10]

3. Attach the randomForest package:

   library(randomForest)

4. Train a random forest model using random_forest =randomForest(Class~., data=GermanCredit_subset):

   random_forest = randomForest(Class~., data=GermanCredit_subset)

5. Invoke importance() for the trained random_forest:

   # Create an importance based on mean decreasing gini

   importance(random_forest)

   The output is as follows:

   importance(random_forest)

                             MeanDecreaseGini

   Duration                         70.380265

   Amount                          121.458790

   InstallmentRatePercentage        27.048517

   ResidenceDuration                30.409254

   Age                              86.476017

   NumberExistingCredits            18.746057

   NumberPeopleMaintenance          12.026969

   Telephone                        15.581802

   ForeignWorker                     2.888387

6. Use the varImp() function to view the list of important variables.

   varImp(random_forest)

   The output is as follows:

                                Overall

   Duration                   70.380265

   Amount                    121.458790

   InstallmentRatePercentage  27.048517

   ResidenceDuration          30.409254

   Age                        86.476017

   NumberExistingCredits      18.746057

   NumberPeopleMaintenance    12.026969

   Telephone                  15.581802

   ForeignWorker               2.888387

   In this activity, we built a random forest model and used it to see the importance of each variable in a dataset. The variables with higher scores are considered more important. Having done this, we can sort by importance and choose the top 5 or top 10 for the model or set a threshold for importance and choose all the variables that meet the threshold.

Activity 14: Selecting Features Using Variable Importance

Solution:

1. Install the following packages:

   install.packages("rpart")

   library(rpart)

   library(caret)

   set.seed(10)

2. Load the GermanCredit dataset:

   data(GermanCredit)

3. Create a subset to load the first ten columns into GermanCredit_subset:

   GermanCredit_subset <- GermanCredit[,1:10]

4. Train an rpart model using rPartMod <- train(Class ~ ., data=GermanCredit_subset, method="rpart"):

   #Train a rpart model

   rPartMod <- train(Class ~ ., data=GermanCredit_subset, method="rpart")

5. Invoke the varImp() function, as in rpartImp <- varImp(rPartMod).

   #Find variable importance

   rpartImp <- varImp(rPartMod)

6. Print rpartImp.

   #Print variable importance

   print(rpartImp)

   The output is as follows:

   rpart variable importance

                             Overall

   Amount                    100.000

   Duration                   89.670

   Age                        75.229

   ForeignWorker              22.055

   InstallmentRatePercentage  17.288

   Telephone                   7.813

   ResidenceDuration           4.471

   NumberExistingCredits       0.000

   NumberPeopleMaintenance     0.000

7. Plot rpartImp using plot().

   #Plot top 5 variable importance

   plot(rpartImp, top = 5, main='Variable Importance')

   The output is as follows:

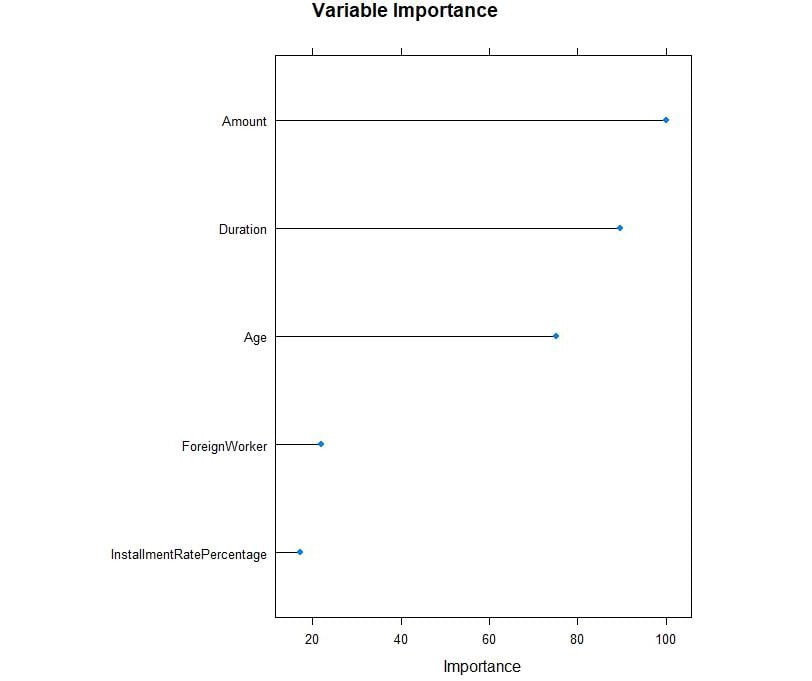
Figure 3.33: Variable importance for the fields

From the preceding plot, we can observe that Amount, Duration, and Age have high importance values.