We have already discussed the advantages of Bayesian statistics over classical statistics in the last chapter. In this chapter, we will see in more detail how some of the concepts of Bayesian inference that we learned in the last chapter are useful in the context of machine learning. For this purpose, we take one simple machine learning task, namely linear regression. Let us consider a learning task where we have a dataset D containing N pair of points  and the goal is to build a machine learning model using linear regression that it can be used to predict values of
and the goal is to build a machine learning model using linear regression that it can be used to predict values of  , given new values of
, given new values of 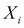 .
.
In linear regression, first, we assume that Y is of the following form:
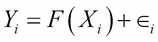
Here, F(X) is a function that captures the true relationship between X and Y, and 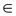 is an error term that captures the inherent noise in the data. It is assumed that this noise is characterized by a normal distribution with mean 0 and variance
is an error term that captures the inherent noise in the data. It is assumed that this noise is characterized by a normal distribution with mean 0 and variance 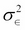 . What this implies is that if we have an infinite...
. What this implies is that if we have an infinite...



