Book Image

Machine Learning Algorithms - Second Edition

Book Image

Machine Learning Algorithms - Second Edition

Overview of this book

Machine learning has gained tremendous popularity for its powerful and fast predictions with large datasets. However, the true forces behind its powerful output are the complex algorithms involving substantial statistical analysis that churn large datasets and generate substantial insight. This second edition of Machine Learning Algorithms walks you through prominent development outcomes that have taken place relating to machine learning algorithms, which constitute major contributions to the machine learning process and help you to strengthen and master statistical interpretation across the areas of supervised, semi-supervised, and reinforcement learning. Once the core concepts of an algorithm have been covered, you’ll explore real-world examples based on the most diffused libraries, such as scikit-learn, NLTK, TensorFlow, and Keras. You will discover new topics such as principal component analysis (PCA), independent component analysis (ICA), Bayesian regression, discriminant analysis, advanced clustering, and gaussian mixture. By the end of this book, you will have studied machine learning algorithms and be able to put them into production to make your machine learning applications more innovative.

Preface

Who this book is for

What this book covers

To get the most out of this book

Free Chapter

A Gentle Introduction to Machine Learning

A Gentle Introduction to Machine Learning

Introduction – classic and adaptive machines

Only learning matters

Beyond machine learning – deep learning and bio-inspired adaptive systems

Machine learning and big data

Important Elements in Machine Learning

Important Elements in Machine Learning

Introduction to statistical learning concepts

Class balancing

Elements of information theory

Feature Selection and Feature Engineering

Feature Selection and Feature Engineering

scikit-learn toy datasets

Creating training and test sets

Managing categorical data

Managing missing features

Data scaling and normalization

Feature selection and filtering

Principal Component Analysis

Independent Component Analysis

Atom extraction and dictionary learning

Visualizing high-dimensional datasets using t-SNE

Regression Algorithms

Regression Algorithms

Linear models for regression

A bidimensional example

Linear regression with scikit-learn and higher dimensionality

Ridge, Lasso, and ElasticNet

Robust regression

Bayesian regression

Polynomial regression

Isotonic regression

Linear Classification Algorithms

Linear Classification Algorithms

Linear classification

Logistic regression

Implementation and optimizations

Stochastic gradient descent algorithms

Passive-aggressive algorithms

Finding the optimal hyperparameters through a grid search

Classification metrics

Naive Bayes and Discriminant Analysis

Naive Bayes and Discriminant Analysis

Naive Bayes classifiers

Naive Bayes in scikit-learn

Discriminant analysis

Support Vector Machines

Support Vector Machines

SVMs with scikit-learn

Kernel-based classification

ν-Support Vector Machines

Support Vector Regression

Introducing semi-supervised Support Vector Machines (S3VM)

Decision Trees and Ensemble Learning

Decision Trees and Ensemble Learning

Binary Decision Trees

Decision Tree classification with scikit-learn

Decision Tree regression

Introduction to Ensemble Learning

Clustering Fundamentals

Clustering Fundamentals

Clustering basics

Gaussian mixture

Evaluation methods based on the ground truth

Advanced Clustering

Advanced Clustering

Spectral Clustering

Online Clustering

Hierarchical Clustering

Hierarchical Clustering

Hierarchical strategies

Agglomerative Clustering

Introducing Recommendation Systems

Introducing Recommendation Systems

Naive user-based systems

Content-based systems

Model-free (or memory-based) collaborative filtering

Model-based collaborative filtering

Introducing Natural Language Processing

Introducing Natural Language Processing

NLTK and built-in corpora

The Bag-of-Words strategy

A sample text classifier based on the Reuters corpus

Topic Modeling and Sentiment Analysis in NLP

Topic Modeling and Sentiment Analysis in NLP

Introducing Word2vec with Gensim

Sentiment analysis

Introducing Neural Networks

Introducing Neural Networks

Deep learning at a glance

MLPs with Keras

Advanced Deep Learning Models

Advanced Deep Learning Models

Deep model layers

An example of a deep convolutional network with Keras

An example of an LSTM network with Keras

A brief introduction to TensorFlow

Creating a Machine Learning Architecture

Creating a Machine Learning Architecture

Machine learning architectures

Scikit-learn tools for machine learning architectures

Other Books You May Enjoy

Other Books You May Enjoy

Leave a review - let other readers know what you think

Customer Reviews

5 star

0

4 star

0

3 star

0

2 star

0

1 star

0

Bayes' theorem

Let's consider two probabilistic events, A and B. We can correlate the marginal probabilities P(A) and P(B) with the conditional probabilities P(A|B) and P(B|A), using the product rule:

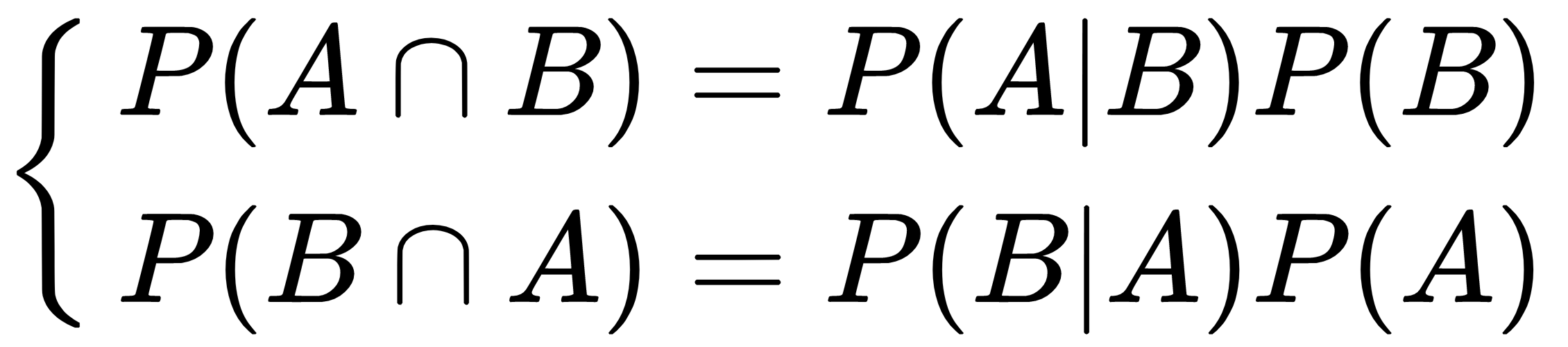
Considering that the intersection is commutative, the first members are equal, so we can derive Bayes' theorem:

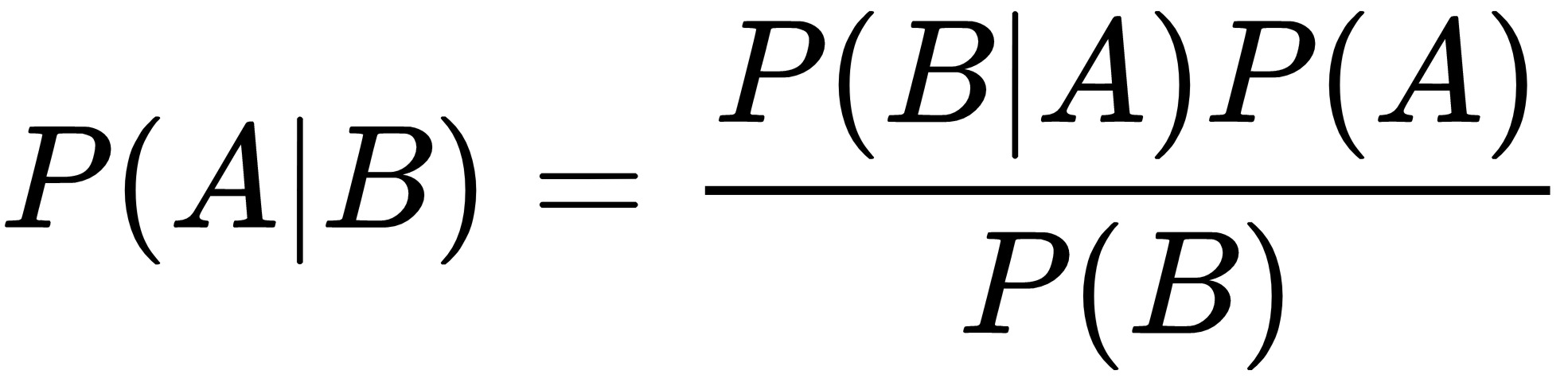
In the general discrete case, the formula can be re-expressed considering all possible outcomes for the random variable A:

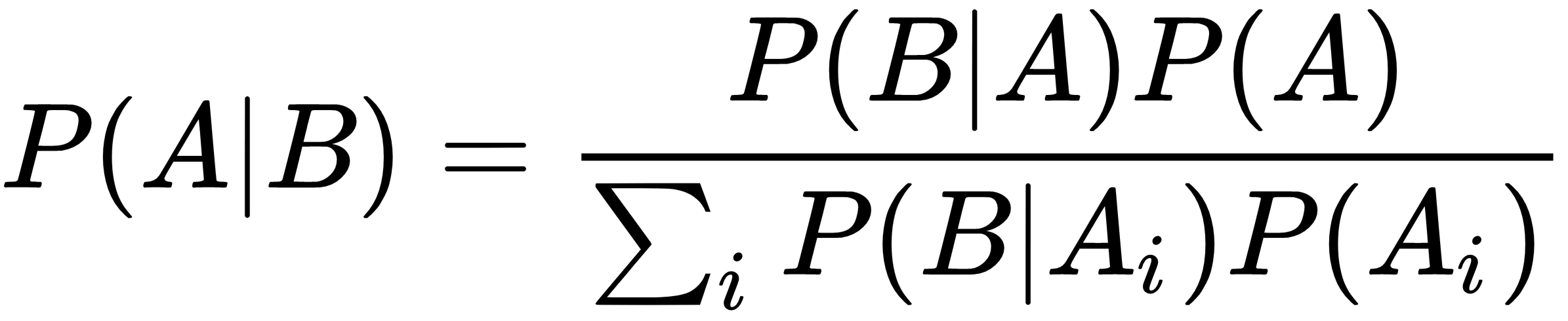
As the denominator is a normalization factor, the formula is often expressed as a proportionality relationship:

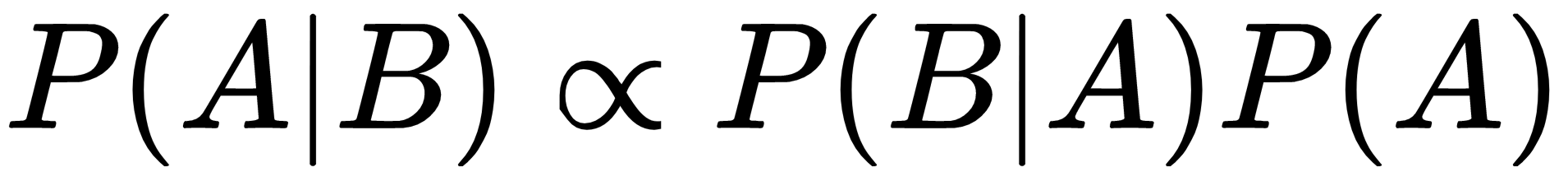
This formula has very deep philosophical implications, and it's a fundamental element of statistical learning. First of all, let's consider the marginal probability, P(A). This is normally a value that determines how probable a target event is, such as P(Spam) or P(Rain). As there are no other elements, this kind...