The binomial tree method was proposed by Cox, Ross, and Robinstein in 1979. Because of this, it is also called the CRR method. Based on the CRR method, we have the following two-step approach. First, we draw a tree, such as the following one-step tree. If we assume that our current stock value is S, there are two outcomes S*u and S*d, where u > 1 and d < 1, as shown in the following code:

import matplotlib.pyplot as plt 
xlim(0,1)
plt.figtext(0.18,0.5,'S')
plt.figtext(0.6,0.5+0.25,'Su')
plt.figtext(0.6,0.5-0.25,'Sd')
plt.annotate('',xy=(0.6,0.5+0.25), xytext=(0.1,0.5), arrowprops=dict(facecolor='b',shrink=0.01))
plt.annotate('',xy=(0.6,0.5-0.25), xytext=(0.1,0.5), arrowprops=dict(facecolor='b',shrink=0.01))
plt.axis('off')

The following is its corresponding graph:

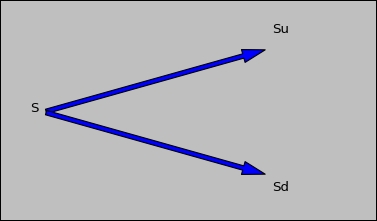
Obviously, the simplest tree is a one-step tree. Assume that today's price is $10, the exercise price is $11, and a call option would mature in six months. In...