Of course, our filter technique is not only limited to black-and-white images. In this section we're going to have a look at color images.
The majority of color images consist of three layers or channels, and this is commonly referred to as RGB, the initialism for the three layers. They are made up of one red channel, one blue channel, and one green channel. When these three channels are laid on top of each other, they add up to create the traditional color image that we know.
Taking that concept, an image is therefore not flat, but actually a cube, a three-dimensional matrix. Combining this idea with our objective, we want to apply a filter to the image, and apply it to all three channels at once. We will, therefore, perform an element-wise multiplication between two three-dimensional cubes.
Our 3x3 filter now has a depth of three and thus nine parameters, plus the bias:
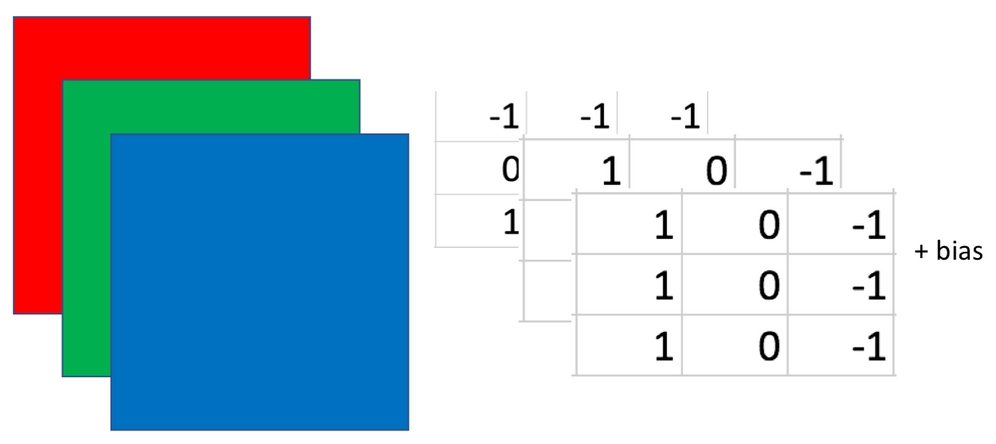
An example of a filter cube or convolutional kernel



