4.3 Generalizing the linear model
The linear model we have been using is a special case of a more general model, the Generalized Linear Model (GLM). The GLM is a generalization of the linear model that allows us to use different distributions for the likelihood. At a high level, we can write a Bayesian GLM like:
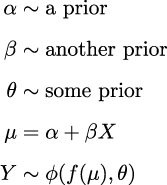
 is an arbitrary distribution; some common cases are Normal, Student’s t, Gamma, and NegativeBinomial. θ represents any auxiliary parameter the distribution may have, like σ for the Normal. We also have f, usually called the inverse link function. When
is an arbitrary distribution; some common cases are Normal, Student’s t, Gamma, and NegativeBinomial. θ represents any auxiliary parameter the distribution may have, like σ for the Normal. We also have f, usually called the inverse link function. When  is Normal, then f is the identity function. For distributions like Gamma and NegativeBinomial, f is usually the exponential function. Why do we need f? Because the linear model will generally be on the real line, but the μ parameter (or its equivalent) may be defined on a different domain. For instance, μ for the NegativeBinomial is defined for positive values, so we need to transform μ....
is Normal, then f is the identity function. For distributions like Gamma and NegativeBinomial, f is usually the exponential function. Why do we need f? Because the linear model will generally be on the real line, but the μ parameter (or its equivalent) may be defined on a different domain. For instance, μ for the NegativeBinomial is defined for positive values, so we need to transform μ....



