5.6 Bayes factors
An alternative to LOO, cross-validation, and information criteria is Bayes factors. It is common for Bayes factors to show up in the literature as a Bayesian alternative to frequentist hypothesis testing.
The Bayesian way of comparing k models is to calculate the marginal likelihood of each model p(y|Mk), i.e., the probability of the observed data Y given the model Mk. The marginal likelihood is the normalization constant of Bayes’ theorem. We can see this if we write Bayes’ theorem and make explicit the fact that all inferences depend on the model.
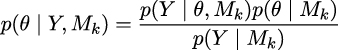
where, y is the data, θ is the parameters, and Mk is a model out of k competing models.
If our main objective is to choose only one model, the best from a set of models, we can choose the one with the largest value of p(y|Mk). This is fine if we assume that all models have the same prior probability. Otherwise, we must calculate:
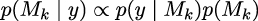
If, instead, our main objective is to compare models to determine which...



