Developing a WebGL game requires a good understanding of 3D mathematics. But we will not cover 3D mathematics in its entirety, since that would require a complete book in itself. In this section, we will cover some basic aspects of 3D mathematics that are required to understand WebGL rendering. We will also build an understanding of the 3D mathematics library that we intend to use in our game. In this section, we will cover a very powerful JavaScript library called glMatrix (http://glmatrix.net).
JavaScript or WebGL do not provide any in-built functions for vector and matrix operations. Hence, we use a third-party library to implement them in our code. glMatrix is designed to perform vector and matrix operations in JavaScript and is extremely fast. So, let's walk through the basics of these operations and also understand their corresponding implementation in glMatrix.
3D game engines use vectors to represent points in space, such as the locations of objects in a game or the vertices of a polygon mesh. They are also used to represent spatial directions, such as the orientation of the camera or the surface normals of a triangle mesh.
A point in 3D space can be represented by a vector using the x, y, and z axes.
WebGL does not provide any functions for matrix or vector operations. Hence, we use third-party libraries for matrix manipulation.
Let's look at some vector operations provided by one of these libraries:
var out=vec3.create() //Creates an empty vector object. var out1=vec3.create() //Creates an empty vector object. var out2=vec3.create() //Creates an empty vector object. var v2=vec3.fromValues(10, 12, 13); //Creates vector initialized with given values. var v3=vec3.fromValues(2,3,4); //Creates vector initialized with given values. vec3.cross(out, v2, v3) //Cross product of vector v2 & v3 placed in vector out. vec3.normalize(out1, v2) // V2 is normalized. Converted to a unit vector and placed in out1. var result=vec3.dot(v2, v3) // Calculates dot product of two vectors. var v4= vec4.fromValues(x, y, z, w)// Creates a vector with w value var v5= vec4(v2, w)
Tip
Downloading the example code
You can download the example code files for all Packt books you have purchased from your account at http://www.packtpub.com. If you purchased this book elsewhere, you can visit http://www.packtpub.com/support and register to have the files e-mailed directly to you.
Matrices are primarily used to describe the relationship between two coordinate spaces in 3D mathematics. They do this by defining a computation to transform vectors from one coordinate space to another, for example, object space to world space or world space to view/camera space.
Some useful matrix operations are:
var mat=mat3.create() //Creates a new identity mat3 var out=mat3.create() //Creates a new identity mat3 mat3.identity(out) //Set a mat3 to the identity matrix var result=mat3.determinant(mat) //Calculates the determinant of a mat3 mat3.invert(out, mat) //Inverts a mat3 mat3.transpose(out, mat) //Transpose the values of a mat3
You will encounter the word "transformation" in all computer graphics books. This word is mostly used to denote change in the object's state. We can apply scaling, rotation, sheer, or translation transformations to change the state of an object. We can apply a combination of the preceding transformations to change the state of the object. The combinations are generally classified as linear or affine transformations.
Linear transformations are the most-used transformations in 3D games. Linear transformations such as scaling, rotation, and sheer will be used throughout your game development career. These transformations are transformations that preserve state, if applied in any order. So, if we scale an object and then rotate it, or first rotate it and then scale it, the end result would be the same. So, transformation is linear, if it preserves the basic operations of addition and multiplication by a scalar.
Some useful functions for linear transformation are:
var a=mat3.create(); var out=mat3.create(); var rad=1.4; //in Radians var v=vec2.fromValues(2,2); mat3.rotate(out, a, rad); //Rotates "a" mat3 by the given angle and puts data in out. mat3.scale(out, a, v) //Scales the mat3 by the dimensions in the given vec2
An affine transformation is a linear transformation followed by translation. Remember that 3 × 3 matrices are used for linear transformations and they do not contain translation. Due to the nature of matrix multiplication, any transformation that can be represented by a matrix multiplication cannot contain translation. This is a problem because matrix multiplication and inversion are powerful for composing complicated transformations. An example of affine transformation is as follows:
var a=mat3.create(); //Identity matrix created var vertex=vec3.fromValues(1,1,1); var scale=mat3.create(); //Identity Matrix created var final=mat3.create(); //Identity Matrix created var factor=vec2.fromValues(2,2); //Scaling factor of double create 2x height and 2x width mat3.scale(scale,a,factor); // a new scale create after multiplication mat3.rotate(final,scale,.4);// new matrix scale created which contains scaling & rotation var newVertex=final*vertex;
In the preceding code, we created a matrix, final, that contained both scaling and rotation operations. We created a composite transformation and applied it on a vertex to get its new position. Now, this final mat3 can be used to transform the vertices of a 3D object. It would be nice if we could find a way to somehow extend the standard 3 × 3 transformation matrix to be able to handle transformations with translation. We can do this by extending our vectors to four-dimensional homogeneous coordinates and using 4 × 4 matrices to transform them. A 4 × 4 matrix is given in the following diagram:
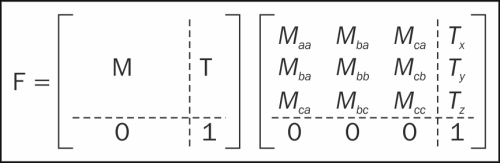
M is the matrix that contains the transformation; the fourth column gives the translation.
Some useful functions for transformations are:
var a=mat4.create();//mat4 identity matrix var final=mat4.create();//mat4 identity matrix var rad=.5; var v=vec3.fromValues(0.5,0.5,0.5); var translate=vec3.fromValues(10,10,10); mat4.rotateX(final, a, rad) //Rotates a matrix by the given angle around the X axis mat4.rotateY(final, final, rad) //Rotates a matrix by the given angle around the Y axis mat4.rotateZ(final, final, rad) //Rotates a matrix by the given angle around the Z axis mat4.scale(final, final, v) //Scales the mat4 by the dimensions in the given vec3 mat4.translate(final, final, v) //Translate a mat4 by the given vector
Now, the final matrix contains composite transformations of rotation along the axis, scaling, and translation.
In a game, when we load or initialize a 3D object, the coordinates of different parts of an object are defined with respect to its pivot point. Let us say our designer created a car in Maya and exported the model. When the model is exported, the coordinate of each wheel is defined with respect to the car body. When we translate or rotate our car, the same transformations have to be applied to the wheels. We then have to project the 3D object on a 2D screen. The projection will not only depend on the location of the camera but also on the lens of the camera. In the following section, we will discuss the two types of transformations, ModelView and projection, to help us implement the rendering of the model on the 2D screen.
Each model or object we want to draw on the scene has coordinates defined with respect to its own origin and axis; we call it object space. When an object is added to the scene and if its own origin coincides with the scene's origin, then its vertices need not be transformed for rendering; but if we want to move the object or rotate it, then we will have to transform its vertices to screen/world coordinates. ModelView transformation is used to transform an object's vertices to world coordinates. An example of this is shown in the following diagram:
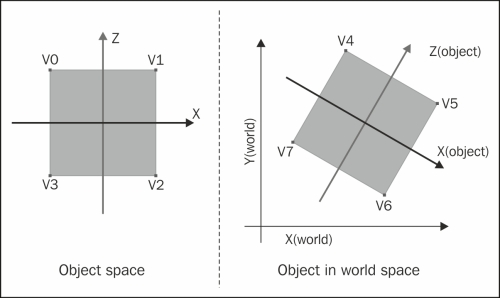
Also, if we move our camera/view around the object, or rotate our camera, then we would need to transform its vertices, changing the world's origin to the camera's position as the origin.
In a nutshell, first model vertices have to be transformed with respect to the scene's origin and then transformed by switching the world's origin to the camera/view position. The final set of all these transformations is maintained as a single 4 x 4 matrix, called the ModelView transformation matrix. The new positions of the model's vertices are obtained via the cross product of each coordinate/vertex of the model with the ModelView transformation matrix, Vf = Mv * V. Here, Vf is the final vector, Mv is the [4 x 4] ModelView matrix, and V is the vector corresponding to each vertex. Each coordinate of a vertex is denoted as [x, y, z, w], where you can put w as 1 for all purposes of this chapter.
Projection transformation is like setting/choosing the lens of the camera. You want to determine the viewing volume of the scene. You want to determine how objects appear and whether the objects are inside the viewing volume or not. The field of view is the parameter that is used to define the viewing volume. Larger values mean you will cover more objects in your game scene; smaller values are like a telephoto lens (the objects will appear closer than they really are). There are two types of projections; orthographic and perspective. In orthographic projection, the objects are mapped directly on the screen without affecting their relative sizes. In perspective projection, the distant objects appear smaller. In gaming, we always use perspective projections. The following diagram explains how our primitive is projected on the screen:
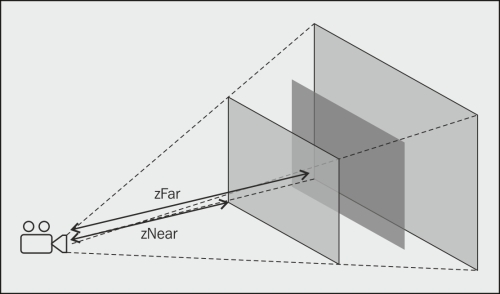
Now, to transform vertices with respect to their distance and chosen lens, we use the projection matrix Vp = P * V. Here, Vp is the final vector, P is the [4 x 4] projection matrix, and V is the vector corresponding to each vertex.
The following is the code to create a projection transformation:
mat4.perspective(out, fovy, aspect, near, far)
The parameters used in the preceding code are:
fovy: Field of viewaspect: Scene aspect rationear: Near plane to create the clipping regionfar: Far plane to create the clipping region
The following code uses the glMatrix library to calculate the perspective matrix using the preceding parameters:
var mat=mat4.create() mat4.perspective(30, gl.viewportWidth / gl.viewportHeight, 0.1, 1000.0, pMatrix);



