A complex number z = x + yi is the sum of a real number x and a real number y multiplied by the imaginary unit i, i 2 = -1 ⇒ i = ±√(-1) , which is the solution of the equation x 2 + 1 = 0.
Complex.h
namespace SmallWindows {
class NotaComplexNumber : public exception {
public:
NotaComplexNumber() {/* Empty. */}
};
extern double Square(double value);
The constructors, assignment operators, and the String conversion operator are similar to their counterparts in Rational:
class Complex {
public:
Complex(double x = 0, double y = 0);
Complex(const Complex &complex);
Complex operator=(const Complex &complex);
bool ReadStream(const String& text);
Complex(const String& text);
operator String() const;
When comparing two complex number, their absolute values (refer to Abs) are compared.
bool operator==(const Complex &complex) const;
bool operator!=(const Complex &complex) const;
bool operator<(const Complex &complex) const;
bool operator<=(const Complex &complex) const;
bool operator>(const Complex &complex) const;
bool operator>=(const Complex &complex) const;
The arithmetic operators apply to complex numbers and double values:
Complex operator+=(double x);
Complex operator+=(Complex &complex);
friend Complex operator+(double x, const Complex &complex);
friend Complex operator+(const Complex &complex, double x);
friend Complex operator+(const Complex &complex1,
const Complex &complex2);
Complex operator-=(double x);
Complex operator-=(Complex &complex);
friend Complex operator-(double x, const Complex &complex);
friend Complex operator-(const Complex &complex, double x);
friend Complex operator-(const Complex &complex1,
const Complex &complex2);
Complex operator*=(double x);
Complex operator*=(Complex &complex);
friend Complex operator*(double x, const Complex &complex);
friend Complex operator*(const Complex &complex, double x);
friend Complex operator*(const Complex &complex1,
const Complex &complex2);
Complex operator/=(double x);
Complex operator/=(Complex &complex);
friend Complex operator/(double x, const Complex &complex);
friend Complex operator/(const Complex &complex, double x);
friend Complex operator/(const Complex &complex1,
const Complex &complex2);
The absolute value of a complex number (and its value converted to a double) is the Pythagoras theorem of the real and imaginary part, that is, the square root of the sum of the squares of the parts:
double Abs() const {return sqrt(Square(x) + Square(y));}
operator double() const {return Abs();}
private:
double x, y;
};
};
Complex.cpp
#include "SmallWindows.h"
namespace SmallWindows {
double Square(double value) {
return value * value;
}
Complex::Complex(double x, double y)
:x(x), y(y) {
// Empty.
}
Complex::Complex(const Complex &complex)
:x(complex.x),
y(complex.y) {
// Empty.
}
Complex Complex::operator=(const Complex &complex) {
x = complex.x;
y = complex.y;
return *this;
}
When interpreting a text holding a rational number, we read the text from a stream, and we need some auxiliary functions to start with. The ReadWhiteSpaces method reads (and disposes of) all white spaces at the beginning of the stream:
void ReadWhiteSpaces(IStringStream& inStream) {
while (true) {
TCHAR tChar = inStream.peek();
if ((tChar >= 0) && (tChar <= 255) && isspace(tChar)) {
inStream.get();
}
else {
break;
}
}
}
The Peek method reads the white spaces and returns the zero character (\0) if it has reached the end of the stream. If not, we look into what comes next in the stream by calling peek, and return its resulting value. Note that peek does not consume the character from the stream; it just checks out the next character:
TCHAR Peek(IStringStream& inStream) {
ReadWhiteSpaces(inStream);
if (inStream.eof()) {
return TEXT('\0');
}
else {
return (TCHAR) inStream.peek();
}
}
The ReadI method verifies whether the next character in the stream is i or I. If it is, it reads the character from the stream and returns true:
bool ReadI(IStringStream& inStream) {
if (tolower(Peek(inStream)) == TEXT('i')) {
inStream.get();
return true;
}
return false;
}
The ReadSign method verifies that the next character in the stream is a plus or minus sign. If it is, it reads the character from the stream, sets the sign parameter to + or -, and returns true:
bool ReadSign(IStringStream& inStream, TCHAR& sign) {
TCHAR tChar = Peek(inStream);
switch (tChar) {
case TEXT('+'):
inStream.get();
sign = TEXT('+');
return true;
case TEXT('-'):
inStream.get();
sign = TEXT('-');
return true;
default:
return false;
}
}
The ReadValue method verifies that the next two characters in the stream are a plus or a minus sign followed by a digit or a dot, or whether the first character is a digit or a dot. If the latter is the case, it reads the value parameter from the beginning of the stream and returns true:
bool ReadValue(IStringStream& inStream, double& value) {
TCHAR tChar = Peek(inStream);
if ((tChar == TEXT('+')) || (tChar == TEXT('-'))) {
inStream.get();
tChar = Peek(inStream);
inStream.unget();
if (isdigit(tChar) || (tChar == TEXT('.'))) {
inStream >> value;
return true;
}
}
else if (isdigit(tChar) || (tChar == TEXT('.'))) {
inStream >> value;
return true;
}
return false;
}
The EndOfLine method simply returns true if the next character in the stream is the zero character (\0), in which case we have reached the end of the string:
bool EndOfLine(IStringStream& inStream) {
return Peek(inStream) == TEXT('\0');
}
Now we are ready to interpret a string as a rational number. We have the following ten cases, where x and y are real values, i is the imaginary unit, and ± is plus or minus. All ten cases represent valid complex numbers:
x ± yi
x ± ±i
x ± i
yi ± x
±i ± x
i ± x
yi
±i
i
x
The ReadStream method creates an input stream from the text and tries to interpret it as one of the preceding ten cases. The idea is that we read the stream and try one part of the potential complex number at a time:
bool Complex::ReadStream(const String& text) {
IStringStream inStream(Trim(text));
double value1, value2;
TCHAR sign1, sign2;
If the stream is made up of a value, a sign, another value, and i or I, we set x and y in accordance with case 1 (x ± yi) and return true. The y field is negative if the sign is minus. However, the second value may also be negative, in which case yis positive:
if (ReadValue(inStream, value1)) {
if (ReadSign(inStream, sign1)) {
if (ReadValue(inStream, value2) && ReadI(inStream) &&
EndOfLine(inStream)) {
x = value1;
y = (sign1 == TEXT('-')) ? -value2 : value2;
return true;
}
If the sign is not followed by a value, but by another sign and i or I, case 2 (x ± ±i) applies and we return true. In this case, we actually have to adjust the value of y twice in accordance with both signs:
else if (ReadSign(inStream, sign2)) {
if (ReadI(inStream) && EndOfLine(inStream)) {
x = value1;
y = (sign1 == TEXT('-')) ? -1 : 1;
y = (sign2 == TEXT('-')) ? -y : y;
return true;
}
}
If the sign is not followed by a value or another sign, but by i or I, case 3 (x ± i) applies and we return true:
else if (ReadI(inStream) && EndOfLine(inStream)) {
x = value1;
y = (sign1 == TEXT('-')) ? -1 : 1;
return true;
}
}
If the value is not followed by a sign but by i or I, another sign, and another value, case 4 (yi ± x) applies and we return true:
else if (ReadI(inStream)) {
if (ReadSign(inStream, sign1)) {
if (ReadValue(inStream, value2) && EndOfLine(inStream)){
y = value1;
x = (sign1 == TEXT('-')) ? -value2 : value2;
return true;
}
}
If the value is followed by i or I and nothing else, case 7 (yi) applies and we return true:
else if(EndOfLine(inStream)) {
y = value1;
x = 0;
return true;
}
}
If the value is followed by nothing else, case 10 (x) applies and we return true:
else if (EndOfLine(inStream)) {
x = value1;
y = 0;
return true;
}
}
If the stream does not start with a value, but with a sign followed by i or I, another sign and another value, case 5 (±i ± x) applies and we return true:
else if (ReadSign(inStream, sign1)) {
if (ReadI(inStream)) {
if (ReadSign(inStream, sign2)) {
if (ReadValue(inStream, value2) && EndOfLine(inStream)){
y = (sign1 == TEXT('-')) ? -1 : 1;
x = (sign2 == TEXT('-')) ? -value2 : value2;
return true;
}
}
If the stream starts with a sign followed by i or I and nothing else, case 8 (±i) applies and we return true:
else if (EndOfLine(inStream)) {
y = (sign1 == TEXT('-')) ? -1 : 1;
x = 0;
return true;
}
}
}
If the stream does not start with a value or a sign, but with i or I followed by a sign and a value, case 6 (i ± x) applies and we return true:
else if (ReadI(inStream)) {
if (ReadSign(inStream, sign2)) {
if (ReadValue(inStream, value2) && EndOfLine(inStream)) {
y = 1;
x = (sign2 == TEXT('-')) ? -value2 : value2;
return true;
}
}
If the stream is made up by i or I and nothing else, case 9 (i) applies and we return true:
else if (EndOfLine(inStream)) {
y = 1;
x = 0;
return true;
}
}
Finally, if none of the above cases apply, the text does not hold a complex number and we return false:
return false; }
The constructor that takes a text simply calls ReadStream and throws a NotaComplexNumber exception if ReadStream returns false. However, if ReadStream returns true, x and y are set to the appropriate values:
Complex::Complex(const String& text) {
if (!ReadStream(text)) {
throw NotaComplexNumber();
}
}
In the String conversion operator, we look into several different cases:
x + i
x - i
x ± i
x
+i
-i
yi
0
If the real part x is not 0, we write its value on the stream and look into the first four cases with regard to the imaginary part, y. If y is plus or minus 1, we simply write +i or -i. If it is not plus or minus 1, and not 0, we write its value with the showpos flag, which forces the plus sign to be present in the case of a positive value. Finally, if y is 0, we do not write it at all:
Complex::operator String() const {
OStringStream outStream;
if (x != 0) {
if (y == 1) {
outStream << x << TEXT("+i");
}
else if (y == -1) {
outStream << x << TEXT("-i");
}
else if (y != 0) {
outStream << x << setiosflags(ios::showpos)
<< y << TEXT("i");
}
else {
outStream << x;
}
}
If x is zero, we omit it and write the value of y in the same manner as we did earlier. However, if y is zero, we write 0; otherwise, nothing will be written if both x and y are 0. Moreover, we omit the showpos flag, since it is not necessary to write the plus sign in the case of a positive value:
else {
if (y == 1) {
outStream << TEXT("i");
}
else if (y == -1) {
outStream << TEXT("-i");
}
else if (y != 0) {
outStream << y << TEXT("i");
}
else {
outStream << TEXT("0");
}
}
return outStream.str();
}
Two complex numbers are equal if their real and imaginary parts are equal:
bool Complex::operator==(const Complex &complex) const {
return ((x == complex.x) && (y == complex.y));
}
bool Complex::operator!=(const Complex &complex) const {
return !(*this == complex);
}
When deciding whether a complex number is smaller than another complex number, we chose to compare their absolute values, which is given by the Abs method:
bool Complex::operator<(const Complex &complex) const {
return (Abs() < complex.Abs());
}
bool Complex::operator<=(const Complex &complex) const {
return ((*this < complex) || (*this == complex));
}
bool Complex::operator>(const Complex &complex) const {
return !(*this <= complex);
}
bool Complex::operator>=(const Complex &complex) const {
return !(*this < complex);
}
The addition operators all call the following final operator, which works for all four arithmetic operators:
Complex Complex::operator+=(double x) {
*this = (*this + Complex(x));
return *this;
}
Complex Complex::operator+=(Complex &complex) {
*this = (*this + complex);
return *this;
}
Complex operator+(double x, const Complex &complex) {
return (Complex(x) + complex);
}
Complex operator+(const Complex &complex, double x) {
return (complex + Complex(x));
}
When adding two complex numbers, we add the real and imaginary parts separately:
Complex operator+(const Complex &complex1,
const Complex &complex2) {
return Complex(complex1.x + complex2.x,
complex1.y + complex2.y);
}
Complex Complex::operator-=(double x) {
return (*this - Complex(x));
}
Complex Complex::operator-=(Complex &complex) {
return (*this - complex);
}
Complex operator-(double x, const Complex &complex) {
return (Complex(x) - complex);
}
Complex operator-(const Complex &complex, double x) {
return (complex - Complex(x));
}
When subtracting two complex numbers, we subtract the real and imaginary parts separately:
Complex operator-(const Complex &complex1,
const Complex &complex2) {
return Complex(complex1.x - complex2.x,
complex1.y - complex2.y);
}
Complex Complex::operator*=(double x) {
*this = (*this * Complex(x));
return *this;
}
Complex Complex::operator*=(Complex &complex) {
*this = (*this * complex);
return *this;
}
Complex operator*(double x, const Complex &complex) {
return (Complex(x) * complex);
}
Complex operator*(const Complex &complex, double x) {
return (complex * Complex(x));
}
The product of two complex numbers can be established by some algebra:
(x 1 + y 1 i)(x 2 + y2i) = x 1 x 2 + x 1 y 2 i + y 1 ix 2 + y 1 y 2 i 2 = x 1 x 2 + x 1 y 2 i + y 1 ix 2 + y 1 y 2 (-1) = x 1 x 2 + x 1 y 2 i + x 2 y 1 i - y 1 y 2 = (x 1 x 2 - y 1 y 2) + (x 1 y 2 + x 2 y 1)i
Complex operator*(const Complex &complex1,
const Complex &complex2) {
return Complex((complex1.x * complex2.x) -
(complex1.y * complex2.y),
(complex1.x * complex2.y) +
(complex2.x * complex1.y));
}
Complex Complex::operator/=(double x) {
*this = (*this / Complex(x));
return *this;
}
Complex Complex::operator/=(Complex &complex) {
*this = (*this / complex);
return *this;
}
Complex operator/(double x, const Complex &complex) {
return (Complex(x) / complex);
}
Complex operator/(const Complex &complex, double x) {
return (complex / Complex(x));
}
The quotient between two complex numbers can also be established by some algebra. The conjugate of a complex number x 2 + y 2 i is x 2 - y 2 i, which we can use in the conjugate rule:
(x 2+ y 2 i)(x 2 - y 2 i) = x 2 2 - x 2 y 2 i + x 2 y 2 i - y 2 2 (-1) = x 2 2 - x 2 y 2 i + x 2 y 2 i + y 2 2 = x 2 2 + y 2 2
We can use the conjugate rule when dividing two complex numbers by multiplying the conjugate by both the numerator and the denominator:
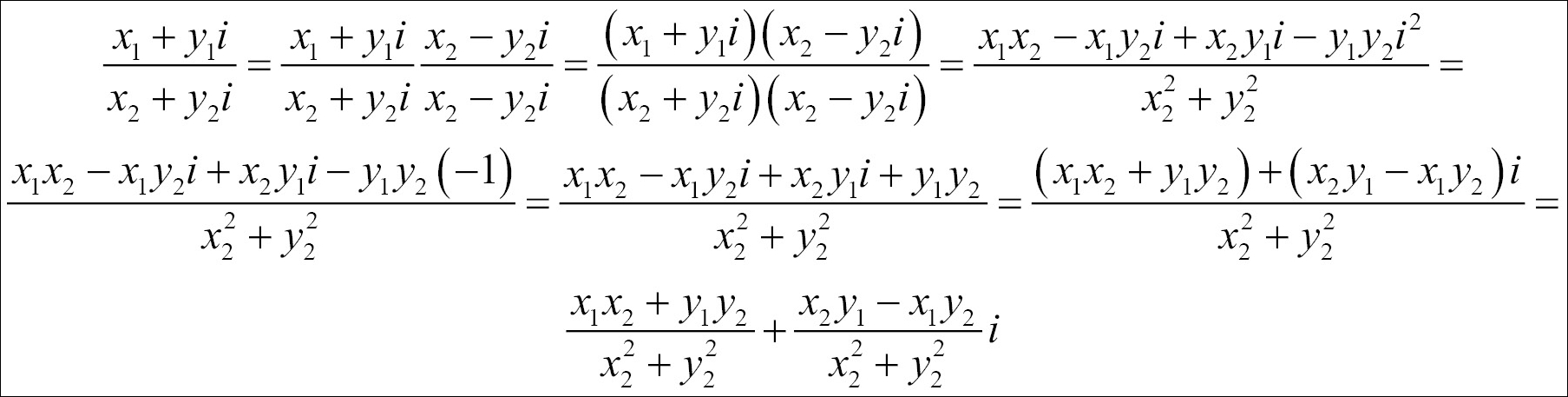
Complex operator/(const Complex &complex1,
const Complex &complex2) {
double sum = Square(complex2.x) + Square(complex2.y);
double x = ((complex1.x * complex2.x) +
(complex1.y * complex2.y)) / sum,
y = ((complex2.x * complex1.y) +
(complex1.x * complex2.y)) / sum;
return Complex(x, y);
}
};



