In this final section, let’s take a look at the computational complexity of algorithms, focusing on both time complexity and space complexity. Why is this so important? Because it can decide whether your algorithm can be used in real-world scenarios. As an example, which of the following do you prefer?
- (A) Absolutely the best route directions to work, but you receive them after an hour, when you are already at work.
- (B) Good enough route directions to work, but you receive them within a few seconds, a moment after you enter your car.
I am sure that you chose B – me too!
Time complexity
First, let’s focus on time complexity, which indicates the amount of time necessary to run an algorithm as a function of the input length, namely n. You can specify it using asymptotic analysis. This includes Big-O notation, which is used to indicate how much time the algorithm will take with the increasing size of the input.
For example, if you search for the minimum value in an unsorted array of size n, you need to visit all elements so that the maximum number of operations is equal to n, which is written as O(n). If the algorithm iterates through each item in a two-dimensional array of size n x n, the time complexity is O(n*n), so it is O(n2).
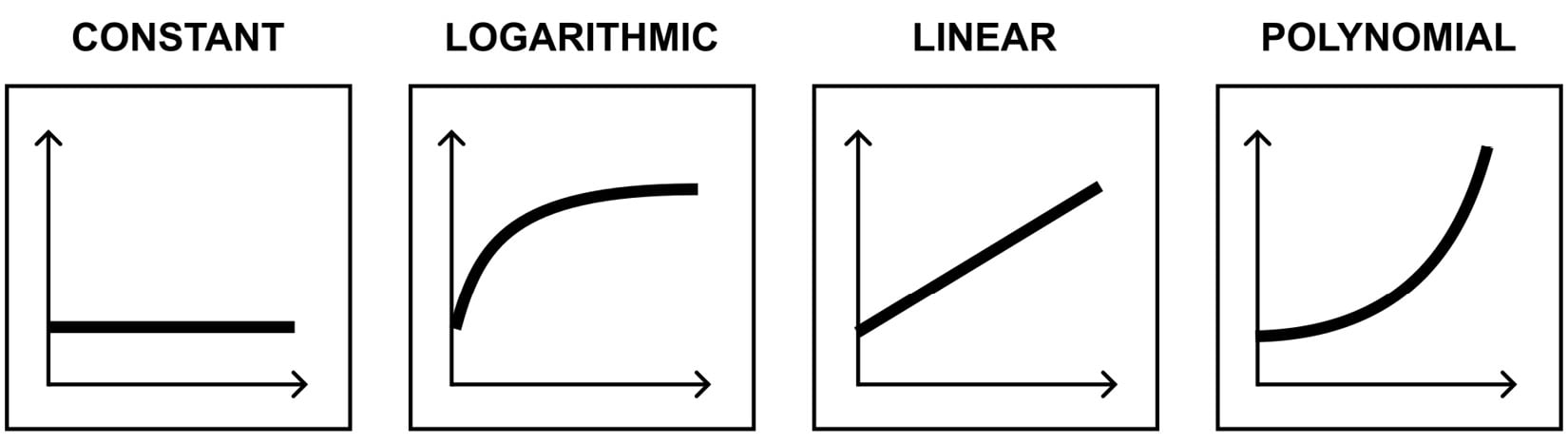
There are various time complexities, including the ones presented here:
Figure 2.5 – Illustration of time complexities
The first is O(1) and is named the constant time. It indicates an algorithm whose execution time does not depend on the input size. The exemplary operations consistent with the O(1) constraint are getting an i-th element from an array, checking whether a hash set contains a given value, or checking whether a number is even or odd.
The next time complexity shown here is O(log n), which is named the logarithmic time. In this case, the execution time is not constant, but it increases slower than in the linear approach. A well-known example of the O(log n) constraint is the problem of finding an item in a sorted array with binary search.
The third case is O(n) and is named the linear time. Here, the execution time increases linearly with the input length. You can take an algorithm for finding the minimum or maximum value in an unordered list or simply finding a given value in an unordered list as examples of the O(n) constraint.
The last time complexity shown here is the polynomial time, which is O(nm), so it can be O(n2) (quadratic time), O(n3) (cubic time), and so on. In this case, the execution time increases much faster than in the case of the linear constraint. It can involve solutions that use nested loops. Examples include the bubble sort, insertion sort, and selection sort algorithms. We'll cover these in Chapter 3, Arrays and Sorting.
Of course, there are even more time complexities available, among which you will find double logarithmic time, polylogarithmic time, fractional power time, linearithmic time, exponential time, and factorial time.
Space complexity
Similar to time complexity, you can specify the space complexity using asymptotic analysis and the Big-O notation. Space complexity indicates how much memory is necessary to run the algorithm with the increasing length of input. You can use similar indicators, such as O(1), O(n), or O(n2).
Where can you find more information?
In this chapter, only a very brief introduction to the subject of algorithms was presented. I strongly encourage you to try to broaden your knowledge regarding algorithms on your own. It is an extremely interesting and challenging topic. For example, you can learn more about various types of algorithms at https://www.techtarget.com/whatis/definition/algorithm and at https://www.geeksforgeeks.org/most-important-type-of-algorithms/, while about the computational complexity at https://en.wikipedia.org/wiki/Computational_complexity. I am keeping my fingers crossed for you success with algorithms!



 Free Chapter
Free Chapter