The Fibonacci series
As the first example, let’s take a look at calculating a given number from the Fibonacci series, using the following recursive function:
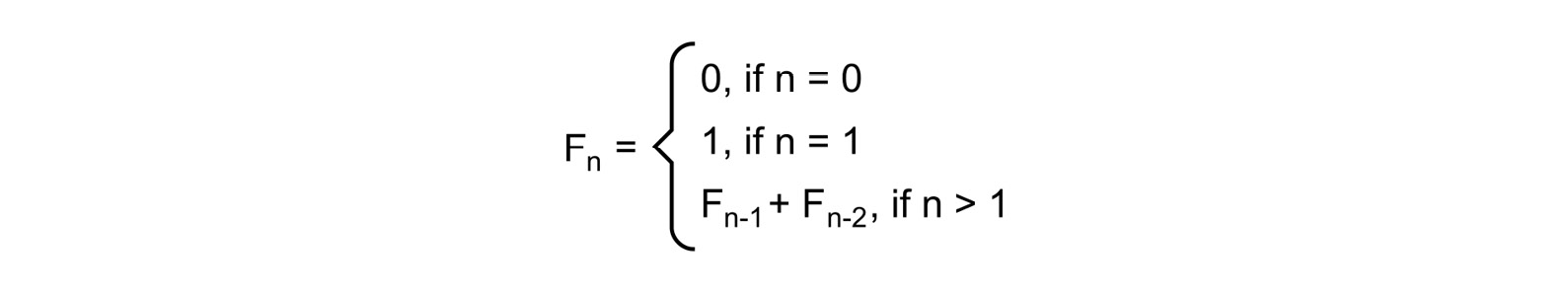
Figure 9.1 – A formula for calculating a number from the Fibonacci series
Its interpretation is very simple:
- F(0) is equal to 0
- F(1) is equal to 1
- F(n) is a sum of F(n-1) and F(n-2), which means that this number is a sum of the two preceding ones
As an example, F(2) is equal to the sum of F(0) and F(1). Thus, it is equal to 1, while F(3) is equal to 2. It is worth mentioning that there are two base cases, namely for n equal to 0 and 1. For both of them, there is a specific value defined, namely 0 and 1.
The recursive implementation in the C# language is shown as follows:
long Fibonacci(int n)
{
if (n == 0) { return 0; }
if (n == 1) { return 1; }
return Fibonacci(n - 1) + Fibonacci(n ...


