In optimization, our goal is to either minimize or maximize a function. For example, a business wants to minimize its costs while maximizing its profits or a shopper might want to get as much as possible while spending as little as possible. Therefore, the goal of optimization is to find the best case of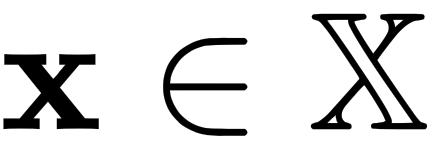 
, which is denoted by x* (where x is a set of points), that satisfies certain criteria. These criteria are, for our purposes, mathematical functions known as objective functions.
For example, let's suppose we have the 
equation. If we plot it, we get the following graph:
You will recall from Chapter 1, Vector Calculus, that we can find the gradient of a function by taking its derivative, equating it to 0, and solving for x. We can find the point(s) at which the function has a minimum or maximum, as follows:
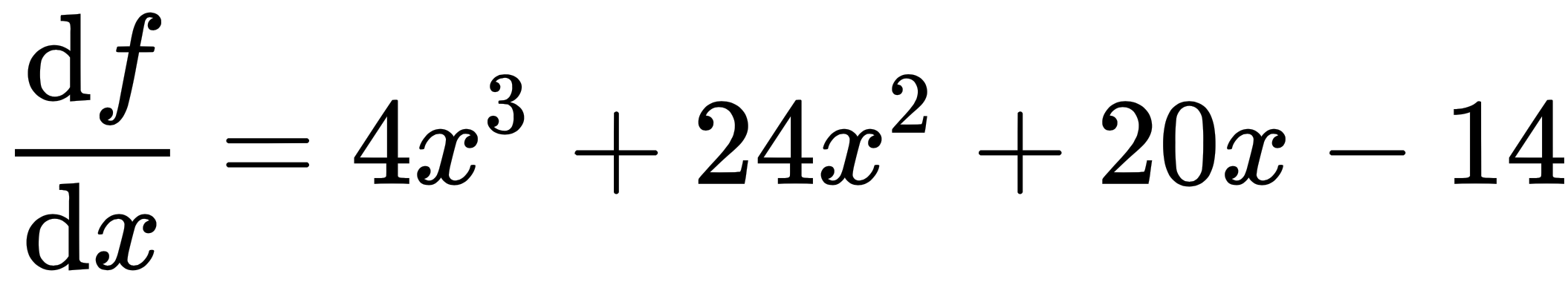
After...
