We saw that time series data is a collection of observations made sequentially along the time dimension. Any time series is, in turn, generated by some kind of mechanism. For example, time series data of daily shipments of your favorite chocolate from the manufacturing plant is affected by a lot of factors such as the time of the year, the holiday season, the availability of cocoa, the uptime of the machines working on the plant, and so on. In statistics, this underlying process that generated the time series is referred to as the DGP. Often, time series data is generated by a stochastic process.
If we had complete and perfect knowledge of reality, all we must do is put this DGP together in a mathematical form and you will get the most accurate forecast possible. But sadly, nobody has complete and perfect knowledge of reality. So, what we try to do is approximate the DGP, mathematically, as much as possible so that our imitation of the DGP gives us the best possible forecast (or any other output we want from the analysis). This imitation is called a model that provides a useful approximation to the DGP.
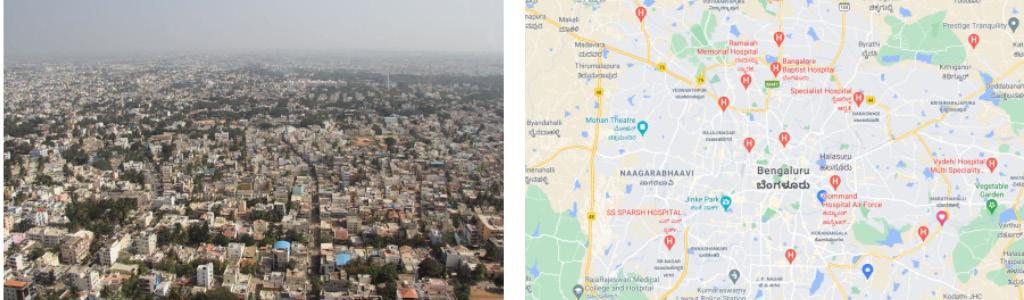
But we must remember that the model is not the DGP, but a representation of some essential aspects of reality. For example, let's consider an aerial view of Bengaluru and a map of Bengaluru, as represented here:
Figure 1.1 – An aerial view of Bengaluru (left) and a map of Bengaluru (right)
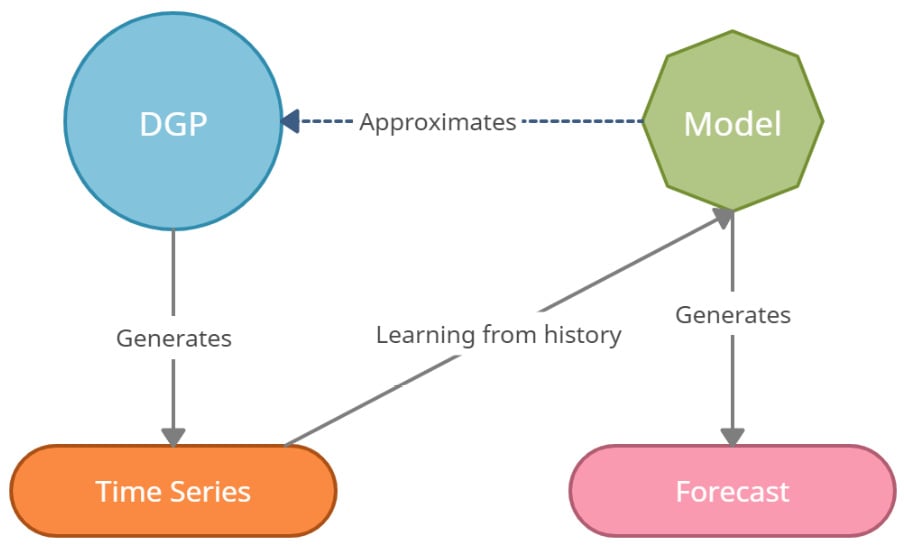
The map of Bengaluru is certainly useful—we can use it to go from point A to point B. But a map of Bengaluru is not the same as a photo of Bengaluru. It doesn't showcase the bustling nightlife or the insufferable traffic. A map is just a model that represents some useful features of a location, such as roads and places. The following diagram might help us internalize the concept and remember it:
Figure 1.2 – DGP, model, and time series
Naturally, the next question would be this: Do we have a useful model? Every model is unrealistic. As we saw already, a map of Bengaluru does not perfectly represent Bengaluru. But if our purpose is to navigate Bengaluru, then a map is a very useful model. What if we want to understand the culture? A map doesn't give you a flavor of that. So, now, the same model that was useful is utterly useless in the new context.
Different kinds of models are required in different situations and for different objectives. For example, the best model for forecasting may not be the same as the best model to make a causal inference.
We can use the concept of DGPs to generate multiple synthetic time series, of varying degrees of complexity.
Generating synthetic time series
Let's take a look at a few practical examples where we can generate a few time series using a set of fundamental building blocks. You can get creative and mix and match any of these components, or even add them together to generate a time series of arbitrary complexity.
White and red noise
An extreme case of a stochastic process that generates a time series is a white noise process. It has a sequence of random numbers with zero mean and constant standard deviation. This is also one of the most popular assumptions of noise in a time series.
Let's see how we can generate such a time series and plot it, as follows:
# Generate the time axis with sequential numbers upto 200
time = np.arange(200)
# Sample 200 hundred random values
values = np.random.randn(200)*100
plot_time_series(time, values, "White Noise")
Here is the output:
Figure 1.3 – White noise process
Red noise, on the other hand, has zero mean and constant variance but is serially correlated in time. This serial correlation or redness is parameterized by a correlation coefficient r, such that:

where w is a random sample from a white noise distribution.
Let's see how we can generate that, as follows:
# Setting the correlation coefficient
r = 0.4
# Generate the time axis
time = np.arange(200)
# Generate white noise
white_noise = np.random.randn(200)*100
# Create Red Noise by introducing correlation between subsequent values in the white noise
values = np.zeros(200)
for i, v in enumerate(white_noise):
if i==0:
values[i] = v
else:
values[i] = r*values[i-1]+ np.sqrt((1-np.power(r,2))) *v
plot_time_series(time, values, "Red Noise Process")
Here is the output:
Figure 1.4 – Red noise process
Cyclical or seasonal signals
Among the most common signals you see in time series are seasonal or cyclical signals. Therefore, you can introduce seasonality into your generated series in a few ways.
Let's take the help of a very useful library to generate the rest of the time series—TimeSynth. For more information, refer to https://github.com/TimeSynth/TimeSynth.
This is a very useful library to generate time series. It has all kinds of DGPs that you can mix and match and create authentic synthetic time series.
Important note
For the exact code and usage, please refer to the associated Jupyter notebooks.
Let's see how we can use a sinusoidal function to create cyclicity. There is a helpful function in TimeSynth called generate_timeseries that helps us combine signals and generate time series. Have a look at the following code snippet:
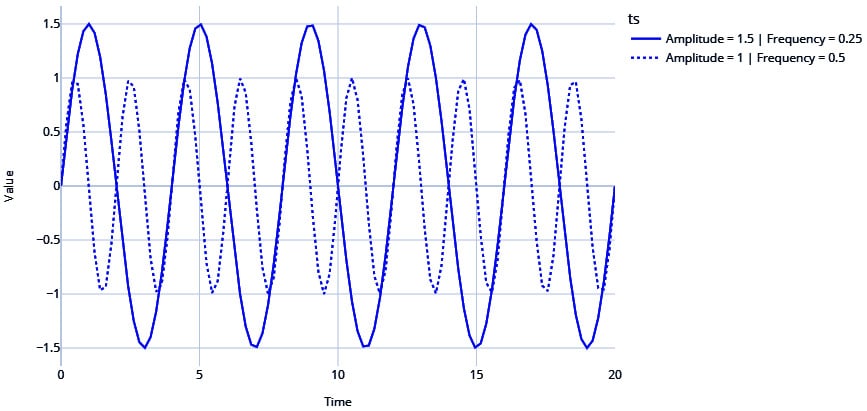
#Sinusoidal Signal with Amplitude=1.5 & Frequency=0.25
signal_1 =ts.signals.Sinusoidal(amplitude=1.5, frequency=0.25)
#Sinusoidal Signal with Amplitude=1 & Frequency=0. 5
signal_2 = ts.signals.Sinusoidal(amplitude=1, frequency=0.5)
#Generating the time series
samples_1, regular_time_samples, signals_1, errors_1 = generate_timeseries(signal=signal_1)
samples_2, regular_time_samples, signals_2, errors_2 = generate_timeseries(signal=signal_2)
plot_time_series(regular_time_samples,
[samples_1, samples_2],
"Sinusoidal Waves",
legends=["Amplitude = 1.5 | Frequency = 0.25", "Amplitude = 1 | Frequency = 0.5"])
Here is the output:
Figure 1.5 – Sinusoidal waves
Note the two sinusoidal waves are different with respect to the frequency (how fast the time series crosses zero) and amplitude (how far away from zero the time series travels).
TimeSynth also has another signal called PseudoPeriodic. This is like the Sinusoidal class, but the frequency and amplitude itself has some stochasticity. We can see in the following code snippet that this is more realistic than the vanilla sine and cosine waves from the Sinusoidal class:
# PseudoPeriodic signal with Amplitude=1 & Frequency=0.25
signal = ts.signals.PseudoPeriodic(amplitude=1, frequency=0.25)
#Generating Timeseries
samples, regular_time_samples, signals, errors = generate_timeseries(signal=signal)
plot_time_series(regular_time_samples,
samples,
"Pseudo Periodic")
Here is the output:
Figure 1.6 – Pseudo-periodic signal
Autoregressive signals
Another very popular signal in the real world is an autoregressive (AR) signal. We will go into this in more detail in Chapter 4, Setting a Strong Baseline Forecast, but for now, an AR signal refers to when the value of a time series for the current timestep is dependent on the values of the time series in the previous timesteps. This serial correlation is a key property of the AR signal, and it is parametrized by a few parameters, outlined as follows:
- Order of serial correlation—or, in other words, the number of previous timesteps the signal is dependent on
- Coefficients to combine the previous timesteps
Let's see how we can generate an AR signal and see what it looks like, as follows:
# Autoregressive signal with parameters 1.5 and -0.75
# y(t) = 1.5*y(t-1) - 0.75*y(t-2)
signal=ts.signals.AutoRegressive(ar_param=[1.5, -0.75])
#Generate Timeseries
samples, regular_time_samples, signals, errors = generate_timeseries(signal=signal)
plot_time_series(regular_time_samples,
samples,
"Auto Regressive")
Here is the output:
Figure 1.7 – AR signal
Mix and match
There are many more components you can use to create your DGP and thereby generate a time series, but let's quickly look at how we can combine the components we have already seen to generate a realistic time series.
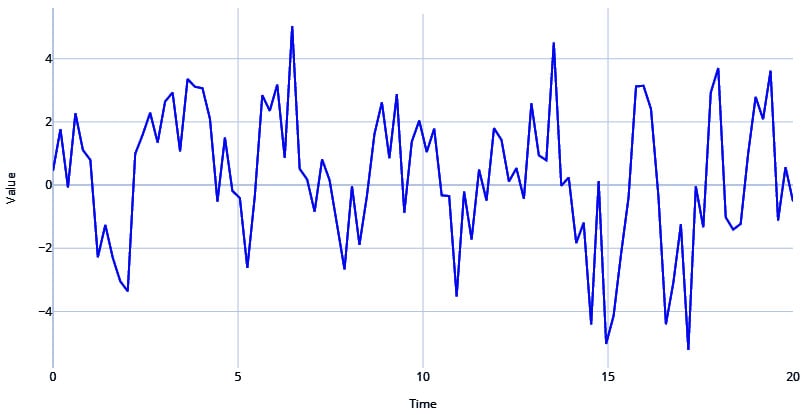
Let's use a pseudo-periodic signal with white noise and combine it with an AR signal, as follows:
#Generating Pseudo Periodic Signal
pseudo_samples, regular_time_samples, _, _ = generate_timeseries(signal=ts.signals.PseudoPeriodic(amplitude=1, frequency=0.25), noise=ts.noise.GaussianNoise(std=0.3))
# Generating an Autoregressive Signal
ar_samples, regular_time_samples, _, _ = generate_timeseries(signal=ts.signals.AutoRegressive(ar_param=[1.5, -0.75]))
# Combining the two signals using a mathematical equation
ts = pseudo_samples*2+ar_samples
plot_time_series(regular_time_samples,
ts,
"Pseudo Periodic with AutoRegression and White Noise")
Here is the output:
Figure 1.8 – Pseudo-periodic signal with AR and white noise
Stationary and non-stationary time series
In time series, stationarity is of great significance and is a key assumption in many modeling approaches. Ironically, many (if not most) real-world time series are non-stationary. So, let's understand what a stationary time series is from a layman's point of view.
There are multiple ways to look at stationarity, but one of the clearest and most intuitive ways is to think of the probability distribution or the data distribution of a time series. We call a time series stationary when the probability distribution remains the same at every point in time. In other words, if you pick different windows in time, the data distribution across all those windows should be the same.
A standard Gaussian distribution is defined by two parameters—the mean and the standard deviation. So, there are two ways the stationarity assumption can be broken, as outlined here:
- Change in mean over time
- Change in variance over time
Let's look at these assumptions in detail and understand them better.
Change in mean over time
This is the most popular way a non-stationary time series presents itself. If there is an upward/downward trend in the time series, the mean across two windows of time would not be the same.
Another way non-stationarity manifests itself is in the form of seasonality. Suppose we are looking at the time series of average temperature measurements in a month for the last 5 years. From our experience, we know that temperature peaks during summer and falls in winter. So, when we take the mean temperature of winter and mean temperature of summer, they will be different.
Let's generate a time series with trend and seasonality and see how it manifests, as follows:
# Sinusoidal Signal with Amplitude=1 & Frequency=0.25
signal=ts.signals.Sinusoidal(amplitude=1, frequency=0.25)
# White Noise with standard deviation = 0.3
noise=ts.noise.GaussianNoise(std=0.3)
# Generate the time series
sinusoidal_samples, regular_time_samples, _, _ = generate_timeseries(signal=signal, noise=noise)
# Regular_time_samples is a linear increasing time axis and can be used as a trend
trend = regular_time_samples*0.4
# Combining the signal and trend
ts = sinusoidal_samples+trend
plot_time_series(regular_time_samples,
ts,
"Sinusoidal with Trend and White Noise")
Here is the output:
Figure 1.9 – Sinusoidal signal with trend and white noise
If you examine the time series in Figure 1.9, you will be able to see a definite trend and the seasonality, which together make the mean of the data distribution change wildly across different windows of time.
Change in variance over time
Non-stationarity can also present itself in the fluctuating variance of a time series. If the time series starts off with low variance and as time progresses, the variance keeps getting bigger and bigger, we have a non-stationary time series. In statistics, there is a scary name for this phenomenon—heteroscedasticity.
This book just tries to give you intuition about stationary versus non-stationary time series. There is a lot of statistical theory and depth in this discussion that we are skipping over to keep our focus on the practical aspects of time series.
Armed with the mental model of the DGP, we are at the right place to think about another important question: What can we forecast?



 Free Chapter
Free Chapter